БЕРНШТЕЙНА МЕТОД

Расстановка ударений: БЕРНШТЕ`ЙНА МЕ`ТОД

БЕРНШТЕЙНА МЕТОД, метод вспомогательных функций, - метод, применяемый в теории линейных и нелинейных дифференциальных уравнений с частными производными. Б. м. состоит в введении нек-рых новых (вспомогательных) функций, зависящих от искомого решения и позволяющих устанавливать для этого решения априорные оценки максимума модуля производных требуемого порядка.

Простым примером применения Б. м. является априорная оценка модуля производных решения задачи Дирихле для нелинейного (квазилинейного) эллиптич. уравнения

(*)

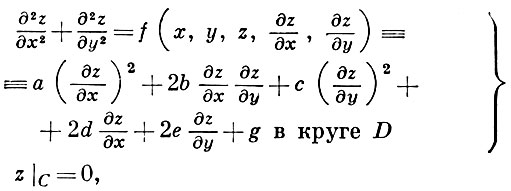
где а, b, с, d, е, g - гладкие функции от х, у, z; С - окружность, граница круга D с радиусом R (предположение о том, что D - круг, a z|_C = 0, не существенно, ибо общий случай произвольной односвязной области и неоднородного граничного условия легко приводятся к рассматриваемому случаю с помощью замены функции и конформного преобразования области).

Если f'_z ≥ 0, то оценка максимума модуля n

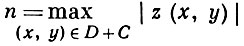
решения задачи (*) сразу получается из принципа максимума.

Для доказательства существования регулярного решения задачи (*) достаточно иметь априорные оценки максимума модуля производных решения до 3-го порядка (см. Продолжения по параметру метод). Для оценки 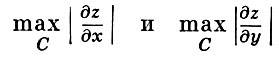достаточно оценить max ∂z/∂ρ (т. к. z|_C = 0), η, θ - полярные координаты в круге D. Пусть введена новая (вспомогательная) функция u по формуле

z = φ₁ (u) = - n - α + α ln u,

где α > 0 будет выбрано позже. Функция u = u(х, у) изменяется от е до e^{(2n + α)/α} и в том же направлении, что и z(x, у) (- n ≤ z ≤ n). Так как

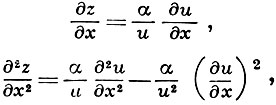
и аналогично для производных по у, то u удовлетворяет уравнению:

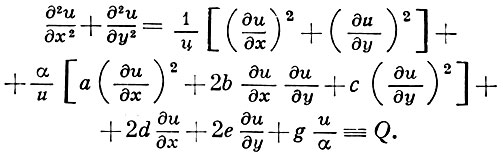
Пусть M - верхняя грань |a|, |b|, |c| в D, a α = 1/8M. Еcли рассматривать 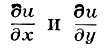как текущие координаты на плоскости, а х, у, z как параметры, то уравнение Q = 0 есть уравнение эллипса, т. к. определитель a₁ c₁ - b₁² > 3/4u², где

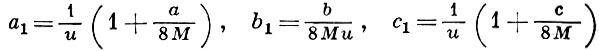
Таким образом, Q при любых 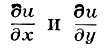и не меньше нек-рого отрицательного числа - Р, Q ≥ - Р (число Р легко указать в явном виде). Если ввести функцию P по формуле

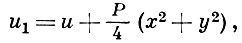
то

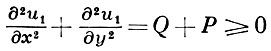
и u₁ достигает максимума на границе С области D, а так как u₁ постоянна на С, то

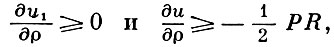
R - радиус окружности С. Отсюда может быть найдена отрицательная нижняя грань для ∂/∂ρ :

Применение тех же рассуждений к другой вспомогательной функции u

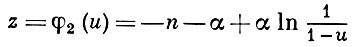
позволяет получить оценку сверху

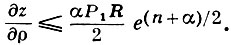
Таким образом, оценивается 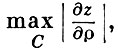, а значит, и 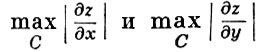. Оценка максимума модуля первых производных внутри области D проводится аналогично: вводится вспомогательная функция u по формуле

z = φ₃ (u) = - n + α ln ln u.

Функция u изменяется в том же направлении, что и z, от е до е^e2n/α . Для u из (*) следует

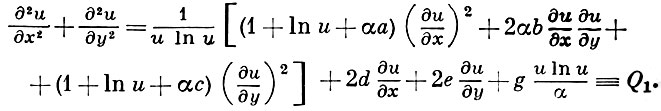
Рассуждения, подобные приведенным, показывают, что если функция

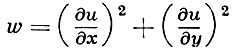
достигает максимума в области D, то этот максимум от n и M. Это дает требуемую оценку 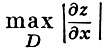и

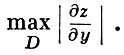
Б. м. позволяет аналогичным образом оценить и максимум модуля в области D + C всех старших производных решения (при этом дополнительно надо лишь дифференцировать исходное уравнение (*)).

Б. м. впервые был применен С. Н. Бернштейном [1]. В дальнейшем Б. м. развивался и систематически употреблялся при изучении различных задач для эллиптических и параболических дифференциальных операторов ([3]-[5]).

Лит. : [1] Бернштейн С. Н., «Math. Ann. », 1906, Bd 62, S. 253-71; 1910, Bd 69, S. 82-136; [2] eго же, Собр. соч., т. 3, М., 1960; [3] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [4] Погорелов А. В., Изгибание выпуклых поверхностей, М. - Л., 1951; [5] Олейник О. Л., Кружков С. Н., «Успехи матем. наук», 1961, т. 16, в. 5, с. 115-55.

И. А. Шишмарёв.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.