БЕРНШТЕЙНА ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС

Расстановка ударений: БЕРНШТЕ`ЙНА ИНТЕРПОЛЯ`ЦИОННЫЙ ПРОЦЕ`СС

БЕРНШТЕЙНА ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС - последовательность алгебраич. многочленов, равномерно сходящаяся на отрезке [- 1, 1] к функции f(x), непрерывной на том же отрезке. Точнее, Б. и. п. - последовательность алгебраич. многочленов

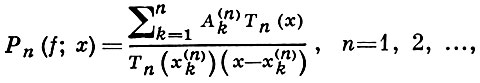
где

Т_n (х) = cos (n arccos х)

- Чебышева многочлены;

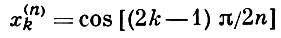
- узлы интерполяции;

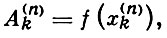
если k ≠ 2ls, l - произвольное натуральное число, n = 2lq + r, q ≥ 1, 0 ≤ r < 2l, s = 1, 2, ..., q;

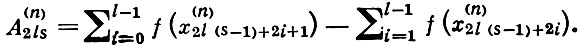
Отношение степени многочлена P_n (f; х) к числу точек, в к-рых P_n (f; х) совпадает с f(x), равно (n - 1)/(n - q), которое при n → ∞ стремится к 2l/(2l - 1); при l достаточно большом этот предел сколь угодно близок к единице. Б. и. п. указан С. Н. Бернштенном в 1931 (см. [1]).

Лит. : [1] Бернштейн С. Н., в кн. : Собр. соч., т. 2, М., 1954, С. 130-40.

П. П. Коровник.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.