БЕРНУЛЛИ ЧИСЛА

Расстановка ударений: БЕРНУ`ЛЛИ ЧИ`СЛА

БЕРНУЛЛИ ЧИСЛА - последовательность рациональных чисел В₀, В₁, В₂, ..., найденная Я. Бернулли [1] в связи с вычислением суммы одинаковых степеней натуральных чисел:

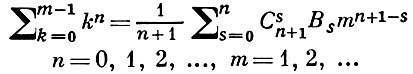
Значения первых Б. ч. :

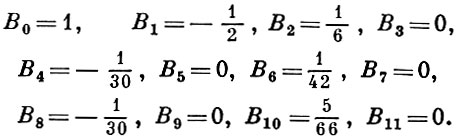
Все Б. ч. с нечетными номерами, кроме В₁, равны нулю, знаки В_2n чередуются. Б. ч. являются значениями при х = 0 Бернулли многочленов: В_n = В_n (0); коэффициентами разложения нек-рых элементарных функций в степенные ряды часто служат Б. ч. Напр.

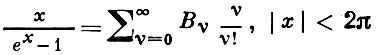
(т. н. производящая функцию для Б. ч.),

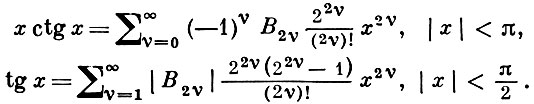
Л. Эйлер (L. Euler, 1740) указал на связь между Б. ч. и значениями дзета-функции Римана ǂ (s) при четных s = 2m:

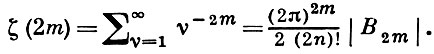
Через Б. ч. выражаются многие несобственные интегралы, напр.

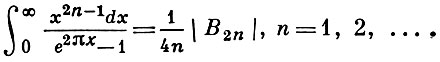
Некоторые соотношения для Б. ч. :

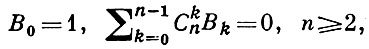
(рекуррентная формула):

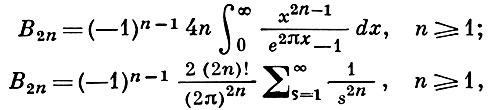
оценка:

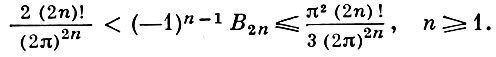
Для Б. ч. имеются обширные таблицы, напр., в [2] приведены точные значения В_2n для n ≤ 90 и приближенные значения для n ≤ 250.

Б. ч. находят многочисленные применения в математич. анализе, теории чисел, приближенных вычислениях.

Лит. : [1] Веrnоulli J., Ars conjectandi, Basileae, 1713; [2] Tables of the higher mathematical functions, v. 2, Bloomington, 1935; [3] Saalsсhuetz L., Vorlesungen iiber die Bernoullischen Zahlen, В., 1893; [4] Чистяков И. И., Бернуллиевы числа, М., 1895; [5] Niеlsеn N., Traite elementaire de nombres de Bernoulli, P., 1923; [6] Кудpявцев В. А., Суммирование степеней чисел натурального ряда и числа Бернулли, М - Л., 1936; [7] Nörlund N. Е., Vorlesungen über Differenzenrechnung, В., 1924; [8] Гeльфонд А. О., Исчисление конечных разностей, 3 изд., М., 1967; [9] Харди Г., Расходящиеся ряды, пер. с англ., М., 1951.

Ю. Н. Субботин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.