БЕРНУЛЛИ МНОГОЧЛЕНЫ

Расстановка ударений: БЕРНУ`ЛЛИ МНОГОЧЛЕ`НЫ

БЕРНУЛЛИ МНОГОЧЛЕНЫ - многочлены вида

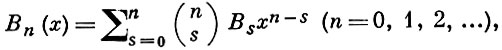
где B_s - Бернулли числа. Так, для n = 0, 1, 2, 3

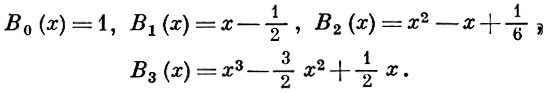
Б. м. можно вычислять по рекуррентной формуле

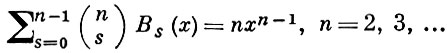
Для натурального х = m Б. м. впервые рассматривались Я. Бернулли (J. Bernoulli, 1713) в связи с вычислением суммы

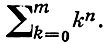
При произвольном х Б. м. впервые изучал Л. Эйлер (L. Euler) (см. [1], с. 390). Термин «Б. м. » ввел И. Л. Раабе (J. L. Baabe, 1851). Основное свойство: Б. м. удовлетворяют разностному уравнению

В_n (х + 1) - В_n (x) = nx^{n - 1}

и поэтому играют в исчислении конечных разностей ту же роль, что и степенные функции в дифференциальном исчислении.

Б. м. принадлежат к классу Аппеля многочленов, т. е. удовлетворяют условию:

В'_n (х) = nВ_{n - 1} (х)

и тесно связаны с Эйлера многочленами:

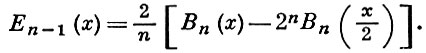
Производящая функция Б. м. имеет вид:

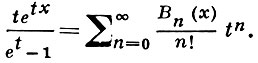
Для Б. м. справедливо разложение в Фурье ряд: для n = 1

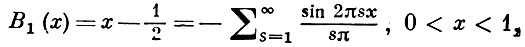
и для n = 2, 3,...

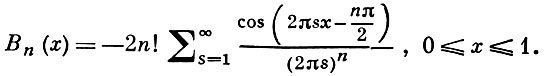
Б. м. удовлетворяют соотношениям:

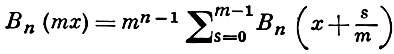
(теорема умножения),

В_n (1 - x) = (- 1)ⁿ B_n (х)

(теорема дополнения),

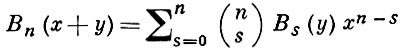
(теорема сложения аргументов).

Б. м. используются для выражения остаточного члена Эйлера-Маклорена формулы суммирования и для разложения функций в ряды. Из свойств Б. м. выводятся многие важные свойства чисел Бернулли. Б. м. используются для интегрального представления дифференцируемых периодич. функций

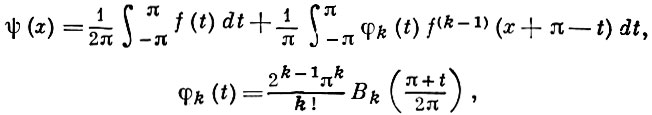
и играют важную роль в теории приближения таких функций тригонометрич. полиномами и др. агрегатами, см. Фавара задача.

Известны различного рода обобщения Б. м. Н. Э. Нёрлундом введены обобщенные Б. м. порядка ν и степени n:

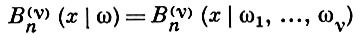
(нек-рые частные случаи этих многочленов рассматривались ранее В. Г. Имшенецким, Н. Я. Сониным и Д. М. Синцовым). Пусть

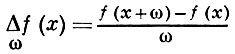
и

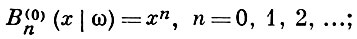
тогда B_n^(ν) (x|ω) последовательно определяются как полиномиальные решения степени n разностного уравнения

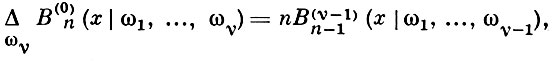
ν = l, 2, ..., с начальными условиями

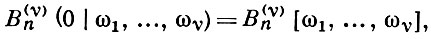
где B_n^(ν) (ω₁, ..., ω_ν) (обобщенные числа Бернулли) находятся из рекуррентного соотношения

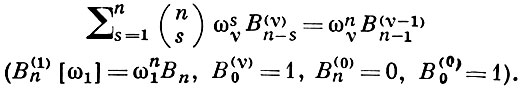
Лит. : [1] Эйлер Л., Дифференциальное исчисление, пер. с лат., М. - Л., 1949; [2] Nörlund N. Е., Vorlesungen über Differenzenrechnung, В., 1924; [3] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра, пер. с англ., М., 1965; [4] Лихин В. В., в сб. : Историко-математические исследования, в. 12, М., 1959, с. 59-134.

Ю. Н. Субботин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.