БЕРНУЛЛИ ИСПЫТАНИЯ

Расстановка ударений: БЕРНУ`ЛЛИ ИСПЫТА`НИЯ

БЕРНУЛЛИ ИСПЫТАНИЯ - независимые испытания с двумя исходами каждое («успехом» и «неудачей») и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей.

Пусть р - вероятность успеха и q = 1 - р - вероятность неудачи, и пусть 1 обозначает наступление успеха, а 0 - наступление неудачи. Тогда вероятность определенного чередования успехов и неудач, напр.,

1 0 0 1 1 0 1 0... 1,

равна

p q q p p q p q... p = p^m q^{n - m},

где m - число успехов в рассматриваемом ряду n испытаний. Со схемой Б. и. связаны многие распространенные распределения вероятностей. Пусть S_n - случайная величина, равная числу успехов в n Б. и. Тогда вероятность события {S_n = k} равна

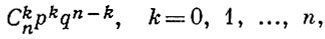
т. е. S_n имеет биномиальное распределение. Последнее при n → ∞ аппроксимируется нормальным распределением или Пуассона распределением. Пусть Y₁ - число испытаний до первого успеха. Тогда вероятность события {Y₁ = k) равна

q^k p, k = 0, 1, 2, ...,

т. е. Y₁ имеет геометрическое распределение. Если Y_r - число неудач, предшествующих r-му появлению успеха, то Y_r имеет так наз. отрицательное биномиальное распределение. Число успехов S_n в Б. и. можно представить в виде суммы X₁ + X₂ + ... + X_n независимых случайных величин, где X_j равно 1, если j-е испытание закончилось успехом, и равно 0 в противном случае. Поэтому многие важные закономерности теории вероятностей, относящиеся к суммам независимых случайных величин, были первоначально установлены для схемы Б. и. (Бернулли теорема, больших чисел закон, больших чисел усиленный закон, повторного логарифма закон, Центральная предельная теорема и т. д.).

Строгое изучение бесконечных последовательностей Б. п. требует введения вероятностной меры в пространстве бесконечных последовательностей нулей и единиц. Это можно сделать или непосредственно, или с помощью приема, к-рый иллюстрируется ниже случаем p = q = 1/2. Пусть ω-число, выбираемое наудачу на отрезке (0, 1) с равномерным распределением, и пусть

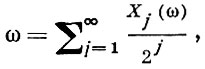
где X_j (ω) = 0 или 1, есть разложение ω в двоичную дробь. Тогда X_j, j = 1, 2, ..., независимы и принимают значения 0 и 1 с вероятностью 1/2 каждое, т. е. чередование нулей и единиц в двоичном разложении ω описывается схемой Б. и. с p = 1/2. Однако меру на (0, 1) можно задать и так, чтобы получить Б. и. с любым р (при р ≠ 1/2 получается мера, сингулярная относительно меры Лебега).

Б. и. часто трактуют геометрически (см. Бернулли блуждание). Ряд вероятностей, связанных с Б. и., был вычислен на самой ранней ступени развития теории вероятностей в связи с задачей о разорении игроков.

Лит. : [1] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М., 1967; [3] Кац М., Статистическая независимость в теории вероятностей, анализе и теории чисел, пер. с англ., М., 1963.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.