
БЕРЕНСА-ФИШЕРА ПРОБЛЕМА
Расстановка ударений: БЕ`РЕНСА-ФИ`ШЕРА ПРОБЛЕ`МА
БЕРЕНСА-ФИШЕРА ПРОБЛЕМА - аналитическая проблема, возникшая в связи со статистич. задачей сравнения по эмпирич. данным математич. ожиданий в двух нормальных распределениях, дисперсии к-рых неизвестны (предполагается, что отношение дисперсий также неизвестно). Эта задача была поставлена В. Беренсом [1] в связи с вопросом обработки данных об урожайности. Современная формулировка Б.-Ф. п. принадлежит Р. Фишеру (R. Fisher) и основана на понятии достаточной статистики. Пусть X11, ..., X1n и X21, ..., X2n - взаимно независимые случайные величины, распределенные нормально, причем ЕX1i = μ1, Е(X1i - μ1)2 = σ12 (i = 1, ..., n1) и ЕX2j = μ2, Е(X2j - μ2)2 = σ22 (j = 1, ..., n2). Предполагается, что значения математич. ожиданий μ1, μ2, дисперсий σ12, σ22, а также их отношения σ12 /σ22 неизвестны. Достаточная статистика в случае n1 ≥ 2, n2 ≥ 2 есть четырехмерный вектор (X¯1, X¯2, S12, S22), компоненты к-рого выражаются формулами
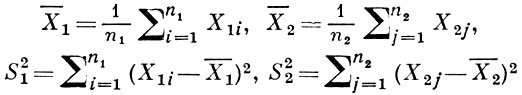
и представляют собой взаимно независимые случайные величины, причем 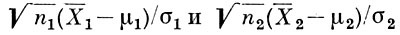 подчиняются стандартному нормальному распределению, а S12 /σ12 и S22 /σ22 - распределению хи-квадрат с n1 - 1 и n2 - 1 степенями свободы соответственно. Поскольку достаточная статистика несет в себе ту же информацию о неизвестных параметрах μ1, μ2, σ12, σ22, что и исходные случайные величины X1i и X2j в количестве n1 + n2, то при проверке гипотез о значениях этих параметров разумно рассматривать лишь достаточную статистику. В частности, это соображение служит основой современной формулировки задачи о проверке гипотезы, согласно к-рой μ1 - μ2 = Δ (Δ - заранее заданное число); при этом Б.-Ф. п. заключается в отыскании такого множества Кα в пространстве возможных значений случайных величин X¯1 - X¯2, S12, S22, чтобы при справедливости проверяемой гипотезы вероятность события (X¯1 - X¯2, S12, S22) ∈ Кα не зависела от всех неизвестных параметров и в точности равнялась наперед заданному числу α из интервала 0 < α < 1.
подчиняются стандартному нормальному распределению, а S12 /σ12 и S22 /σ22 - распределению хи-квадрат с n1 - 1 и n2 - 1 степенями свободы соответственно. Поскольку достаточная статистика несет в себе ту же информацию о неизвестных параметрах μ1, μ2, σ12, σ22, что и исходные случайные величины X1i и X2j в количестве n1 + n2, то при проверке гипотез о значениях этих параметров разумно рассматривать лишь достаточную статистику. В частности, это соображение служит основой современной формулировки задачи о проверке гипотезы, согласно к-рой μ1 - μ2 = Δ (Δ - заранее заданное число); при этом Б.-Ф. п. заключается в отыскании такого множества Кα в пространстве возможных значений случайных величин X¯1 - X¯2, S12, S22, чтобы при справедливости проверяемой гипотезы вероятность события (X¯1 - X¯2, S12, S22) ∈ Кα не зависела от всех неизвестных параметров и в точности равнялась наперед заданному числу α из интервала 0 < α < 1.
Вопрос о существовании решения Б.-Ф. п. долгое время дискутировался видными математиками (главным образом в связи с предложенным Р. Фишером подходом к этой проблеме, по существу выходящим за рамки теории вероятностей). В 1964 Ю. В. Линник (совместно с учениками) доказал, что при объемах выборок n1 и n2 разной четности решение Б.-Ф. п. Кα существует. Вопрос же о существовании решения для n1 и n2 одинаковой четности остался открытым.
Б.-Ф. п. неоднократно подвергалась видоизменениям и обобщениям. В частности, А. Вальд (A. Wald) предложил задачу об отыскании множества Кα в пространстве двух переменных (X¯1 - X¯2)S12 и S12 /S22 . Вопрос о существовании такого решения остается открытым. Однако можно эффективно построить такое множество K*α, что в случае справедливости проверяемой гипотезы μ1 - μ2 = Δ вероятность события ((X¯1 - X¯2)S12 и S12 /S22) ∈ K*α хотя и будет зависеть от неизвестного отношения σ12 /σ22, но ее отклонение от заданного α будет мало. Это обстоятельство и служит основой современных рекомендаций для практич. построения критериев сравнения μ1 и μ2 .
Простые и удобные в вычислительном отношении критерии для сравнения μ1 и μ2 предложены В. И. Романовским, М. Бартлеттом (М. Bartlett), Г. Шеффе (Н. Scheffe) и др. Однако статистики этих критериев в терминах достаточной статистики не выражаются и поэтому имеют, вообще говоря, меньшую мощность, чем критерии, конструируемые с помощью решения Б.-Ф. п. и ее обобщений.
Лит. : [1] Вehrens W. U., «Landwirtsch. Jahrb. », 1929, Bd 68, № 6, S. 807-37; [2] Линник Ю. В., Статистические задачи с мешающими параметрами, М., 1966; [3] Линник Ю. В., Романовский И. В., Судаков В. Н., «Докл. АН СССР», 1964, т. 155, № 6, с. 1262-64.
Л. Н. Большев.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'