БЕРГМАНА-ВЕЙЛЯ ПРЕДСТАВЛЕНИЕ

Расстановка ударений: БЕ`РГМАНА-ВЕ`ЙЛЯ ПРЕДСТАВЛЕ`НИЕ

БЕРГМАНА-ВЕЙЛЯ ПРЕДСТАВЛЕНИЕ, Бергмана-Вейля формула, Вейля формула, - интегральное представление голоморфных функций, полученное А. Вейлем и С. Бергманом (см. [1], [2]) и определяемое следующим образом. Пусть D - область голоморфности в _j, функции W₁, ..., W_n голоморфны в D и V = {z ∈ D: |W_k (z)| < 1, k = 1, ..., N}⋐ D. Тогда любую функцию f, голоморфную в V и непрерывную в V¯ в любой точке z ∈ V, можно представить формулой

(*)

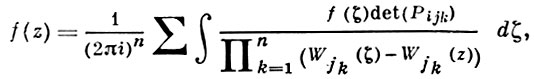
где суммирование производится по всем j₁ <... < j_n, а интегрирование - по соответствующим образом ориентированным n-мерным поверхностям σ_{j1, ..., jn}, образующим остов области V (см. Аналитический полиэдр), dζ = dζ₁ ∧... ∧ dζ_n, а функции Р_ij (ζ, z) голоморфны в области D × D и определяются в соответствии с Xефера теоремой (см. [3], с. 245) из равенств

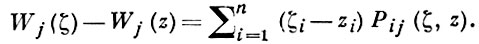
Интегральное представление (*) наз. представлением Бергмана-Вейля.

Области V, фигурирующие в Б.-В. п., наз. областями Вейля; обычно для них требуется дополнительное условие, чтобы ранги матриц (∂W_iν /∂z_μ), ν = 1, ..., k, μ = 1, ..., n, k ≤ n, на соответствующих множествах

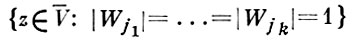
были максимальными (= k) для всех j₁ <... < j_k (такие области Вейля наз. регулярными). Области Вейля в Б.-В. п. можно заменить аналитическими полиэдрами

U = {z ∈ D: W_j (z) ∈ D_j, j = 1, ..., N} ⋐ D,

где D_j - ограниченные области с кусочно гладкими границами ∂D_j на плоскости С. Б.-В. п. определяет значение голоморфной функции f внутри аналитич. полиэдра U по значениям f на его остове σ ; при n > 1 размерность о строго меньше размерности ∂U. При n = 1 аналитич. полиэдры вырождаются в области с кусочно гладкими границами, остов и граница совпадают, а если еще N = 1 и W(z) = z, то Б.-В. п. совпадает с интегральной формулой Коши.

Важным свойством Б.-В. п. является голоморфность (по z) его ядра. Поэтому если вместо голоморфной функции f поставить произвольную интегрируемую на о функцию, то правая часть Б.-В. п. даст функцию, голоморфную всюду в U и почти всюду в D\∂U; такие функции наз. интегралами типа Бергмана-Вейля. Если f голоморфна в U и непрерывна в Ū, то ее интеграл типа Бергмана-Вейля равен нулю почти всюду в D\Ū.

Из Б.-В. п. в области Вейля V после замены

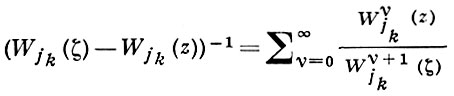
получается разложение Вейля

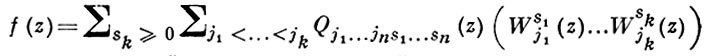
в ряд по функциям, голоморфным в области D, и этот ряд сходится равномерно на компактных подмножествах V.

Лит. : [1] Wеil A., «Math. Ann. », 1935, Bd 111, S. 178-82; [2] Вergman S., «Матем., сб. », 1936, т. 1, с. 242-57; [3] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964.

Е. М. Чирка.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.