БЕРГМАНА КЕРНФУНКЦИЯ

Расстановка ударений: БЕ`РГМАНА КЕРНФУ`НКЦИЯ

БЕРГМАНА КЕРНФУНКЦИЯ - функция комплексных переменных, обладающая свойством воспроизводящего ядра и определяемая для любой области D ⊂ ℂⁿ, в к-рой существуют голоморфные функции f ≢ 0, принадлежащие классу L² (D) по мере Лебега dV. Введена С. Бергманом [1]. Множество указанных функций f образует гильбертово пространство L_h² (D) ⊂ L² (D) с ортонормированным базисом {φ₁, φ₂,...}; L_h² (D) = L² (D) ∩ O(D), где O(D) - пространство голоморфных функций. Функция

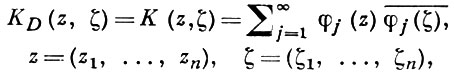
наз. Б. к. (или просто кернфункцией) области D. Ряд справа равномерно сходится на компактных подмножествах D и принадлежит L_h² (D) при каждом фиксированном его сумма не зависит от выбора ортонормированного базиса {φ_j}. Б. к. зависит от 2n комплексных переменных и определена в области D × D ⊂ ℂ²ⁿ ; она обладает свойством симметрии К(ζ, z) = K¯ (z, ζ), голоморфна по переменным z и антиголоморфна по ζ. Если D = D' × D'', D' ⊂ ℂ^m, D'' ⊂ ℂ^{n - m}, то

K_D (z, ζ) = K_D' (z', ζ ') K_D'' (z'', ζ ''),

где z' = (z₁, ..., z_m), z'' = (z_{m + 1}, ..., z_n).

Основным свойством Б. к. является ее воспроизводящее свойство: для любой функции f ∈ L_h² (D) и любой точки z ∈ D справедливо интегральное представление

f(z) = ∫_D f (ζ) K (z, ζ) dV (ζ).

Экстремальные свойства Б. к. 1) Для любой точки z ∈ D

K (z, z) = sup { |f(z)|² : f ∈_h² (D), ||f||_{L² (D)} ≤ 1}.

2) Пусть точка ζ ∈ D такова, что в классе L_h² (D) имеются функции с условием f(ζ) = 1. Тогда функция K(z, ζ)/K(ζ, ζ) удовлетворяет этому условию и имеет норму K(ζ, ζ)^{- 1/2}, минимальную для всех таких й Функция K(z, ζ)/K(ζ, ζ) наз. экстремальной функцией области D.

Изменение Б. к. при биголоморфных отображениях выражается в следующей теореме: если φ - биголоморфное отображение области D на область D*, φ (z) = w, φ (ζ) = η, то

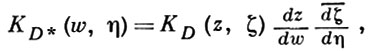
где dz/dw - якобиан обратного отображения. Благодаря этому свойству эрмитова квадратичная форма

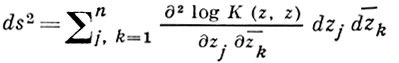
инвариантна относительно биголоморфных отображений.

Функция K(z) = K(z, z), к-рую также наз. кернфункцией, играет значительную роль во внутренней геометрии областей. В общем случае она неотрицательная, а функция log K(z) плюрисубгармоническая. В областях D, для к-рых K(z) положительная (напр., в ограниченных областях), функции K(z) и log К(z) строго плюрисубгармонические. Последнее эквивалентно тому, что в таких областях D указанная форма ds² положительно определена и, следовательно, задает в D эрмитову риманову метрику. Эта метрика не меняется при биголоморфных отображениях и наз. метрикой Бергмана. Ее можно рассматривать как частный случай Кэлера метрики. Из экстремального свойства 1) следует, что коэффициенты метрики Бергмана неограниченно возрастают при подходе к нек-рым граничным точкам. Если D ⊂ ℂⁿ - строго псевдовыпуклая область или аналитич. полиэдр, то K(z)неограниченно возрастает при любом подходе z к границе области D. Всякая область, обладающая этим свойством Б. к., является областью голоморфности.

Для простейших областей Б. к. вычисляется в явном виде. Напр., Б. к. для шара В: |z| < R в ℂⁿ имеет вид:

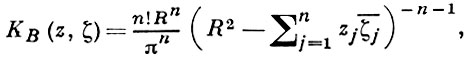
для поликруга U: |z_j | < R_j, j = 1, ..., n, в ℂⁿ :

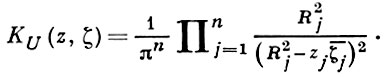
В частном случае, когда n = 1 и область U есть круг |z| < R на комплексной плоскости z, метрика Бергмана обращается в классическую гиперболич. метрику

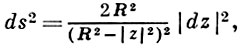
инвариантную относительно конформных отображений и определяющую в U геометрию Лобачевского.

Лит. : [1] Bergman S., The kernel function and conformal mapping, N. Y., 1950; [2] Фукс Б. А., Специальные главы теории аналитических функций многих комплексных переменных, М., 1963; [3] Шабат Б. В., Введение в комплексный анализ, М., 1969, ч. 2, гл. 4.

Е. М. Чирка.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.