БЕНДИКСОНА КРИТЕРИЙ

Расстановка ударений: БЕ`НДИКСОНА КРИТЕ`РИЙ

БЕНДИКСОНА КРИТЕРИЙ - теорема, позволяющая установить отсутствие замкнутых траекторий у динамич. систем на плоскости:

х' = Р (х, у), y' = Q (x, у). (*)

Впервые был указан И. Бендиксоном [1] в следующей формулировке: если в односвязной области G выражение Р'_x + Q'_y знакопостоянно (т. е. сохраняет знак и обращается в нуль лишь в отдельных точках или на нек-рых кривых), то система (*) не имеет в области G замкнутых траекторий. Обобщение Б. к. принадлежит А. Дюлаку [2]: если G - односвязная область в плоскости х, у, функции Р и Q ∈ C¹ (G) и если найдется такая функция f(x, y) ∈ C¹ (G), что

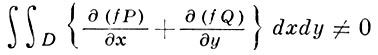
для любой односвязной подобласти D ⊂ G, то в области G не существует ни одной простой спрямляемой замкнутой кривой, составленной из траекторий и особых точек системы (*). В случае кольцеобразной области G аналогичная теорема утверждает единственность замкнутой траектории (если она существует) системы (*). Возможно обобщение на случай системы (*) с цилиндрич. фазовым пространством (см. [3]).

Лит. : [1] Bendixson I., «Acta Math. », 1901, Bd 24, 1, S. 1-88; [2] Dulас H., «C. r. Acad. sci. », 1937, t. 204, № 23, p. 1703-06; [3] Андpонов А. А., Витт А. А., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959.

Н. X. Розов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.