БЕМОЛЬНАЯ ФОРМА

Расстановка ударений: БЕМО`ЛЬНАЯ ФО`РМА

БЕМОЛЬНАЯ ФОРМА - измеримая r-мерная дифференциальная форма ω на открытом множестве R ⊂ Eⁿ такая, что:

комасса |ω |₀ ≤ N₁ для нек-рого N₁ ;

существует N₂ с

|∫_{∂σ r + 1} ω | ≤ N₂ |σ^{r + 1} |

для любого симплекса σ^{r + 1}, удовлетворяющего условию: существует измеримое Q ⊂ R, |R\Q|_n = 0 такое, что со измерима на σ^{r + 1} и на любой из его граней σ^r, составляющих ∂σ^{r + 1}, причем

|σ^{r + 1} |\Q|_{r + 1} = 0, |σ^r \Q|_r = 0;

здесь |M|_s означает s-мерную - меру Лебега пересечения множества М с нек-рой s-мерной плоскостью.

Если X есть r-мерная бемольная коцепь в R, то существует ограниченная r-мерная форма ω_X в R, измеримая в любом симплексе σ^r относительно плоскости, содержащей σ^r, и

Хσ^r = ∫_σ^r ω_X, (1)

причем |ω_X |₀ = |X|, |ω_dX |₀ = |dX|,

где |X| - комасса коцепи X. Обратно, любой r-мерной Б. ф. ω в R соответствует по формуле (1) единственная r-мерная бемольная коцепь X_ω для любого симплекса σ^r, удовлетворяющего вышеуказанному условию, причем

|X_ω | ≤ N₁, |dX_ω | ≤ N₂ .

Форма ω и коцепь X наз. ассоциированными. Формы, ассоциированные с одной и той же коцепью, эквивалентны, т. е. равны почти всюду в R, и среди них есть бемольный представитель.

Между n-мерными бемольными коцепями X и классами эквивалентных измеримых ограниченных функций φ (р) существует взаимно однозначное соответствие, при к-ром ω_X = φ (р) dp, а

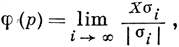
где - ω₁, ω₂, ... - последовательность n-мерных симплексов, стягивающихся к точке р так, что их диаметры → 0, но

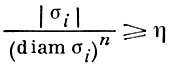
при нек-ром η для всех i, |σ_i | - объем σ₁ .

Пусть α (р) - измеримая суммируемая функция в R, значениями к-рой являются r-векторы; она наз. соответствующей r-мерной бемольной цепи А, если

∫_R ω_X ⋅ α = X ⋅ A (2)

для всех r-мерных бемольных коцепей X (и тогда A наз. лебеговой цепью). Отображение α → А является линейным взаимно однозначным отображением множества классов эквивалентности функций α (р) в пространство бемольных цепей C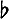_r (R), причем |A| = ∫_R |α |₀, где |A| - масса цепи А, |α |₀ - масса r-вектора α (р). Кроме того, множество образов непрерывных функций α плотно в C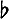_r (R).

Представления (1) и (2) обобщают аналогичные результаты для диезных форм и диезных коцепей; напр., дифференциал Б. ф. ω_X, определяемый формулой dω_X = ω_dXω является также Б. ф., и выполнена теорема Стокса: ∫_∂σ ω = ∫_σ dω для любого симплекса σ; r-мерная бемольная коцепь - слабый предел гладких коцепей, т. е. таких, для к-рых ассоциированные формы ω являются гладкими, и т. д.

Лит. : [1] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960.

М. И. Войцеховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.