
БЕМОЛЬНАЯ НОРМА
Расстановка ударений: БЕМО`ЛЬНАЯ НО`РМА
БЕМОЛЬНАЯ НОРМА r-мерной полиэдральной цепи А в пространстве Еn - норма |А| , определяемая следующим образом:
, определяемая следующим образом:
|А| = inf { |A - ∂D| + |D| },
= inf { |A - ∂D| + |D| },
где |С| - масса цепи С, ∂С - ее граница, и нижняя грань берется по всем (r + 1)-мерным полиэдральным цепям. Свойства Б. н. :
|аА| = |a||А|
= |a||А| , |А + В|
, |А + В| ≤ |A|
≤ |A| + |В|
+ |В| ,
,
|А| = 0 ⇔ А = 0, |А|
= 0 ⇔ А = 0, |А| ≤ |A|, |σ |
≤ |A|, |σ | = |τ |
= |τ |
для любой клетки σ, если π - проекция Еn на нек-рую плоскость, то |π А| ≤ |А|
≤ |А| .
.
Пополнение линейного пространства полиэдральных цепей Сr (Еn) является сепарабельным банаховым пространством Сr {Еn); элементы его наз. r-мерными бемольными цепями, и каждой из них можно приписать конечную или бесконечную массу:
{Еn); элементы его наз. r-мерными бемольными цепями, и каждой из них можно приписать конечную или бесконечную массу:
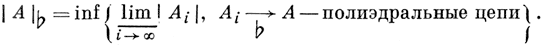
Граница ∂бемольной цепи также определяется предельным переходом, она является непрерывной операцией, и
|∂А| ≤ |А|
≤ |А| , |А|
, |А| = inf {|А - ∂D|
= inf {|А - ∂D| + |D|
+ |D| }.
}.
Б. н. представляет собой наибольшую из полунорм | ⋅ |' в Сr (Еn), удовлетворяющую для любой клетки σ неравенствам: |σr |' ≤ |σr |, |∂σr + 1 ]' ≤ |σr + 1 |. r-мерная бемольная коцепь X - линейная функция r-мерных бемольных цепей А (обозначается через X ⋅ A) такая, что (|X| - комасса X)
|X ⋅ А| ≤ N |A| для нек-рого N.
для нек-рого N.
Она является элементом сопряженного с Сr {Еn) пространства С
{Еn) пространства С r {Еn), к-рое оказывается несепарабельным. Бемольная норма |X|
r {Еn), к-рое оказывается несепарабельным. Бемольная норма |X| -мерной бемольной коцепи X определяется стандартным образом:
-мерной бемольной коцепи X определяется стандартным образом:
|X| = sup |X ⋅ A|, |А|
= sup |X ⋅ A|, |А| = 1
= 1
так что
|А| = sup |X ⋅ A| и |X ⋅ A | ≤ |X|
= sup |X ⋅ A| и |X ⋅ A | ≤ |X| |A|
|A| ,
,
|X| = 1
= 1
причем
|X| ≤ |X| .
.
Для кограницы dX бемольной коцепи (определяемой условием: dX ⋅ A = X ⋅ dA): |dX| ≤ |X|
≤ |X| , так что |X|
, так что |X| = sup {|X|, |dX|}.
= sup {|X|, |dX|}.
Аналогичные понятия вводятся для полиэдральных r-мерных цепей, расположенных в открытых подмножествах R ⊂ En . См. также Бемольная форма.
Лит. : [1] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960.
М. И. Войцеховский.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'