БЕЙТМЕНА ФУНКЦИЯ

Расстановка ударений: БЕ`ЙТМЕНА ФУ`НКЦИЯ

БЕЙТМЕНА ФУНКЦИЯ, k-функция, - функция

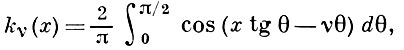
(1)

где x и ν - действительные числа; определена Г. Бейтменом [1]. Б. ф. может быть выражена с помощью вырожденной гипергеометрич. функции 2-го рода ψ (а, b, x):

Г (ν + 1) k_2ν (x) = e^{- x} ψ (- ν, 0; 2x), x > 0. (2)

Соотношение (2) удобно принять в качестве определения Б. ф. в комплексной плоскости с разрезом (0, ∞). Справедливы следующие соотношения: для случая (1)

k_ν (- x) = k_{- ν} (x),

для случая (2)

k_2ν (- ξ ± i0) = k_{- 2ν} (ξ) - e^{±ν π i} ⋅ e^ξ Ф (- ν, 0, - 2ξ),

где ξ > 0, Ф (а, b; x) - вырожденная гипергеометрич. функция 1-го рода.

Лит. : [1] Bateman H., «Trans. Amer. Math. Soc. », 1931, v. 33, p. 817-31; [2] Бeйтмeн Г., Эрдейи А., Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра, пер. с англ., 2 изд., М., 1973.

Л. Н. Кармазина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.