БЕЙЕСОВСКИЙ ПОДХОД ЭМПИРИЧЕСКИЙ

Расстановка ударений: БЕЙЕ`СОВСКИЙ ПОДХО`Д ЭМПИРИ`ЧЕСКИЙ

БЕЙЕСОВСКИЙ ПОДХОД ЭМПИРИЧЕСКИЙ - статистич. интерпретация бейесовского подхода к построению выводов о ненаблюдаемых значениях случайных параметров при неизвестном их априорном распределении. Пусть (Y, X) - случайный вектор, причем предполагается, что плотность р(у|х) условного распределения Y при любом заданном значении случайного параметра X = x известна. Если в результате нек-рого эксперимента наблюдается лишь реализация Y, а соответствующая реализация X неизвестна и требуется оценить значение заданной функции φ (X) от ненаблюдаемой реализации, то согласно Б. п. э. в качестве приближенного значения ψ (Y) для φ (X) следует использовать условное математич. ожидание Е{φ (X)|Y}, к-рое в силу Бейеса формулы выражается отношением

ψ (Y) = [∫ ψ (х) р (Y | x) р (x) dμ (x)] / q (Y), (1)

где

q(y) = ∫ p (y | x) p (x) dμ (x), (2)

р(x) - плотность безусловного (априорного) распределения X, μ (x) - соответствующая σ-конечная мера; функция q (y) представляет собой плотность безусловного распределения Y.

Если априорная плотность р (x) неизвестна, то вычисление значений ψ и q невозможно. Однако, если имеется достаточно большое количество реализаций независимых случайных величин Y₁, ..., Y_k, подчиняющихся распределению с плотностью q(y), то для q(y) можно построить состоятельную оценку q^(y), зависящую лишь от Y₁, ..., Y_k . Для оценки значения ψ (Y) С. Н. Бернштейн [1] предложил заменить в (2) q(у) на q^(y) и найти решение р^ (x) этого интегрального уравнения, а затем подставить р^ и q^ в правую часть (1). Однако этот путь затруднителен, так как решение указанного интегрального уравнения принадлежит к числу некорректно поставленных задач вычислительной математики.

В нек-рых исключительных случаях статистич. подход может быть применен не только для оценки q, но и ψ (см. [3]). Такая возможность возникает тогда, когда справедливо тождество относительно x и y

φ (х) p (y | x) = λ (y) r [z (y) | x], (3)

где λ (y) и z (y) - функции, зависящие лишь от у, a r (z | x) как функция от z является плотностью вероятности (т. е. ее можно рассматривать как плотность условного распределения нек-рой случайной величины Z при заданном значении X = x). Если (3) справедливо, то числитель отношения (1) равен произведению λ (Y)s[z(Y)], где s(z) = ∫ r (z | x) p (x) dμ (x) - плотность безусловного распределения Z. Т. о., если имеется достаточно большое количество реализаций независимых случайных величин Z₁, ..., Z_m, подчиняющихся распределению с плотностью s (z), то для s (z) можно построить состоятельную оценку s (z), а значит, и найти состоятельную оценку ψ ^(Y) для ψ (Y):

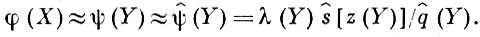
(4)

Напр., если требуется оценить φ (X) = Х^h (h целое > 0), причем р (у | х) = х^y е^{- x} /y! (у = 0, 1, 2,...; x > 0), то φ (x) p (y | x) = λ (y) p (y + h | x), где λ (y) = (y + h)! / y!. Так как здесь r (z | x) = p (z | x), то s (z) = q (z). Поэтому ψ ^(Y) - = λ (Y) q^ (Y + h) / q^ (Y), т. е. для отыскания ψ ^ нужна лишь последовательность реализаций Y₁, Y₂,.... Если же p (у | х) = b_n (y | х) = C^y_n x^y (1 - х)^{n - y} (у = 0, 1, n; n целое > 0; 0 ≤ x ≤ 1), то φ (x)p(y | x) = λ (y) r (y + h | x), где λ (y) = C^y_n /C^{y + h}_{n + h} и r (z | x) = b_{n + h} (z | x) ≠ p (z | x). Поэтому для построения ψ ^ (Y) в этом случае нужно иметь две последовательности эмпирических значений Y_i и Z_j .

Указанная методика Б. п. э. применима к весьма узкому классу плотностей р (у | х) и функций φ (x), Удовлетворяющему условию (3); и если даже это условие выполняется, то для построения оценки (4) нужно располагать реализациями случайных величин Z_j, распределение к-рых, как правило, отлияно от распределения непосредственно наблюдаемых величин Y_i . Для практич. целей предпочтительнее видоизмененная методика Б. п. э., лишенная указанных недостатков. Суть этого видоизменения заключается в построении не самой состоятельной оценки для ψ (Y) (эта оценка может и не существовать), а нижней и верхней оценок для этой функции, отыскание к-рых сводится к решению задачи линейного программирования следующим образом. Пусть Ψ₁ (Y) и Ψ (Y) - условные минимум и максимум линейного функционала (относительно неизвестной априорной плотности р (x)) в числителе (1), вычисленные при линейных условиях р (x) ≥ 0, ∫ р (x) dμ (x) = 1 и q (Y) = ∫ р (Y | x) p (x) dμ (x) = q^ (Y) (q^ (Y) - упомянутая выше оценка для q(Y), построенная по результатам наблюдений Y₁, ..., Y_k). В таком случае можно заключить, что Ψ₁ (Y)/q^(Y) ≤ ψ (Y) ≤ Ψ₂ (Y)/q^(Y), причем вероятность справедливости такого заключения в силу больших чисел закона стремится к единице при неограниченном увеличении количества случайных величин Y_i, используемых при построении оценки q^(Y). Возможны и другие видоизменения Б. п. э., напр., за счет добавления к последнему условию q(Y) = q^(Y) конечного числа условий вида q(y_i) = q^(y_i), где y_i - заранее заданные числа; если q заменить соответствующими доверительными пределами для q, то получаются условия в виде неравенств q₁ (y_i) ≤ q(y_i) ≤ q₂ (y_i) и т. д.

В нек-рых практически важных случаях для функций Ψ₁ и Ψ₂ удается найти удовлетворительные мажоранты, вычисляемые без применения трудоемких методов линейного программирования (см. пример, посвященный статистич. контролю, в ст. Выборочный метод).

О применении Б. п. э. к решению задач статистич. проверки гипотез о значениях случайных параметров см. Дискриминантный анализ.

Лит. : [1] Бернштейн С. Н., «Изв. АН СССР. Сер. матем. », 1941, т. 5, с. 85-94; [2] Большев Л. Н., в кн. : Международный конгресс математиков в Ницце, 1970. Доклады советских математиков, М., 1972, с. 48-55; [3] Robbins Н., в кн. : Proceedings Berkeley Symposium Mathematical Statistics and Probability, v. 1, Berk.-Los Ang., 1956, p. 157-63.

Л. H. Большев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.