БЕЙЕСОВСКИЙ ПОДХОД

Расстановка ударений: БЕЙЕ`СОВСКИЙ ПОДХО`Д

БЕЙЕСОВСКИЙ ПОДХОД к статистическим задачам - подход, основанный на предположении, что всякому параметру в статистич. проблеме принятия решения приписано нек-рое распределение вероятностей. Всякая общая статистич. проблема принятия решения определяется следующими элементами: пространством (X, 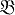_X) выборок x, пространством (Θ, 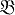_Θ) значений неизвестного параметра θ, семейством распределений вероятностей {P_θ, θ ∈ Θ } на (X, 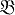_X), пространством решений (D, 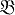_D) и функцией L(θ, d), характеризующей потери от принятия решения d, когда истинное значение параметра есть θ. Цель же проблемы принятия решения состоит в отыскании в определенном смысле наилучшего правила (решающей функции) δ = δ (x), сопоставляющей каждому результату наблюдения x ∈ X решение δ (x) ∈ D. При Б. п., когда считается, что неизвестный параметр θ является случайной величиной с заданным (априорным) распределением π = π (dθ) на (θ, 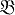_θ), наилучшая решающая функция (бейесовская решающая функция) δ * = δ *(x) определяется как функция, на к-рой достигаются минимальные полные потери inf ρ (π, δ), где

ρ (π, δ) = ∫_Θ ρ (θ, δ) π (dθ)

а

ρ (θ, δ) = ∫_X L(θ, δ (x))P_θ (dx).

Таким образом,

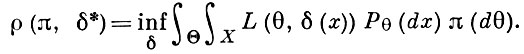
При отыскании бейесовской решающей функции δ * = δ *(x) полезным оказывается следующее замечание. Пусть P_θ (dx) = p(x|θ)dμ (x), π (dθ) = π (θ)dν (θ), где μ и ν - некоторые σ-конечные меры. Тогда, предполагая возможным смену порядков интегрирования, находим

∫_Θ ∫_X P_θ (dx) π (dθ) = ∫_Θ ∫_X L (θ, δ (x)) p(x|θ) π (θ) dμ (x) dν (θ) = ∫_X dμ (x) [∫_Θ L(θ, δ (x)) p(x|θ) π (θ) ν (θ)].

Отсюда видно, что для данного x ∈ X δ * (x) есть то значение d*, на к-ром достигается

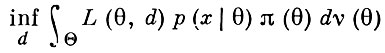
или, что эквивалентно,

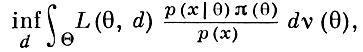
где

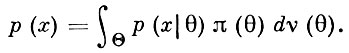
Но по Бейеса формуле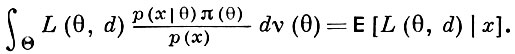

Тем самым для данного x δ * (x) есть то значение d*, на к-ром достигают минимума условные средние потери Е[L(θ, d)|x].

Пример (Б. п. в задаче различения двух простых гипотез). Пусть Θ = {θ₁, θ₂}, D = {d₁, d₂}, L_ij = L(θ_i, d_j), i, j = 1, 2; π (θ₁) = π₁, π (θ₂) = π₂, π₁ + π₂ = 1. Отождествляя решение d_i с принятием гипотезы H_i : θ = θ_i, естественно считать, что L₁₁ < L₁₂, L₂₂ < L₂₁ . Тогда

ρ (π, δ) = ∫_X [τ₁ p (x | θ₁) L (θ₁, δ (x)) + τ₂ p (x | θ₂) L (θ₂, δ (x))] dμ (x),

откуда следует, что inf ρ (π, δ) достигается на функции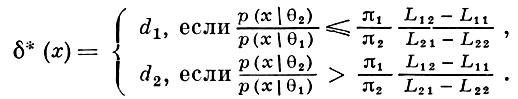

Преимущество Б. п. состоит в том, что полные потери ρ (π, δ) оказываются числом (в отличие от потерь ρ (θ, δ), зависящих от неизвестного параметра θ), и, следовательно, заведомо существуют, если и не оптимальные, то, по крайней мере, ε-оптимальные (ε > 0) решающие функции δ *, для к-рых

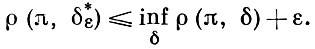
Недостатком Б. п. является необходимость постулировать как существование априорного распределения для неизвестного параметра, так и знание его формы (в определенной степени последнее обстоятельство преодолевается в рамках бейесовского подхода эмпирического).

Лит. : [1] Вальд А., Статистические решающие функции, в сб. : Позиционные игры, М., 1967, с. 300-522; [2] Де Гроот М., Оптимальные статистические решения, пер. с англ., М., 1974.

А. Н. Ширяев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.