БЕЙЕСОВСКАЯ ОЦЕНКА

Расстановка ударений: БЕЙЕ`СОВСКАЯ ОЦЕ`НКА

БЕЙЕСОВСКАЯ ОЦЕНКА - оценка неизвестного параметра по результатам наблюдений при бейесовском подходе. При таком подходе к задачам статистич. оценивания обычно предполагается, что неизвестный параметр θ ∈ Θ ⊆ ℝ^k является случайной величиной с заданным (априорным) распределением π = π (dθ), пространство решений D совпадает с множеством Θ, а потери L(θ, d) отражают расхождение между значением 9 и его оценкой d. Поэтому, как правило, считается, что функция L(θ, d) имеет вид L(θ, d) = a(θ)λ (θ - d), где λ - некоторая неотрицательная функция от вектора погрешностей θ - d. В случае k = 1 часто полагают λ (θ - d) = |θ - d|^α, α > 0; при этом наиболее употребительной и математически более удобной оказывается квадратичная функция потерь Р(θ, d) = |θ - d|² . Для такой функции потерь Б. о. (бейесовская решающая функция) δ * = δ *(x) определяется как функция, на к-рой достигаются минимальные полные потери

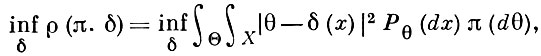
или, что эквивалентно, минимальные условные потери

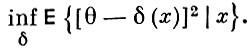
Отсюда следует, что в случае квадратичной функции потерь Б. о. δ * (х) совпадает с апостериорным средним: δ * (ж) = Е (θ |x), а бейесовский риск

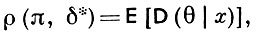
где D(θ |x) - дисперсия апостериорного распределения:

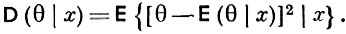
Пример. Пусть x = (x₁, ..., x_n), где x₁, ..., x_n - независимые одинаково распределенные случайные величины, имеющие нормальные распределения N(θ, σ²), σ² известно, а неизвестный параметр θ имеет нормальное распределение N (μ, τ²). Поскольку апостериорное распределение для θ (при заданном х) является нормальным N(μ_n, τ_n²) с

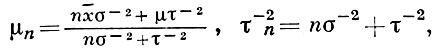
где x¯ = (x¯₁ + ... + x¯_n)/n, то в случае квадратичной функции потерь |θ - d|² бейесовская оценка δ * (x) = μ_n, а бейесовский риск равен τ_n² = σ² τ² /(nτ² + σ²).

А. Н. Ширяев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.