БЕЙЕСА ФОРМУЛА

Расстановка ударений: БЕЙЕ`СА ФО`РМУЛА

БЕЙЕСА ФОРМУЛА - формула, позволяющая вычислять апостериорные вероятности событий (или гипотез) через априорные вероятности. Пусть A₁, ..., A_n - полная группа несовместимых событий: ∪ A_i = Ω, А_i ∩ A_j = ∅ при i ≠ j. Тогда апостериорная вероятность Р(А_i |B) события А_i при условии, что произошло событие В (с Р(B) > 0), может быть найдена по формуле Бейеса:

(*)

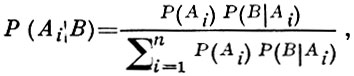
где Р(A_i) - априорная вероятность события А_i, Р(В|A_i) - условная вероятность события В при условии, что произошло событие A_i (с Р(А_i) > 0). Б. ф. доказана Т. Бейесом (Т. Bayes, опубликована в 1763).

Формула (*) является частным случаем следующего абстрактного варианта Б. ф. Пусть θ и ξ - случайные элементы со значениями в измеримых пространствах (θ, Р_θ) и (X, В_X) и E|g(θ)| < ∞. Для всякого множества А ∈ F_ξ = σ {ω : ξ (ω)} положим

G(А) = ∫_Ω g(θ (ω)) E [I_A (ω)|F_θ ] (ω) P (dω),

где F_θ = Ω {ω : θ (ω)} и I_A (ω) - индикатор множества А. Тогда мера G абсолютно непрерывна относительно меры 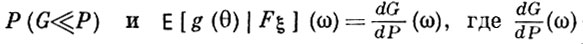- производная Радона-Никодима меры G по мере Р.

Лит. : [1] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974.

А. Н. Ширяев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.