БЕЗИКОВИЧА ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ

Расстановка ударений: БЕЗИКО`ВИЧА ПОЧТИ` ПЕРИОДИ`ЧЕСКИЕ ФУ`НКЦИИ

БЕЗИКОВИЧА ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ - класс (В^p - п. п.) почти периодических функций, в к-ром справедлив аналог теоремы Рисса-Фишера: любой тригонометрич. ряд

∑_n a_n e^{iλ_n x},

где

∑_n |a_n |² < ∞,

служит рядом Фурье нек-рой В² - п. п. функции. Определение Б. п. п. ф. (А. С. Безикович [1], [2]), основанное на обобщении понятия почти периода, требует введения нек-рых дополнений. Множество Е действительных чисел наз. достаточно однородным, если существует L > 0 такое, что отношение наибольшего количества членов Е в интервале длины L к наименьшему количеству в том же интервале L меньше 2. Достаточно однородное множество является относительно плотным. Комплексная функция f(x), - ∞ < x < ∞, суммируемая со степенью р в каждом конечном интервале действительной оси, наз. Б. п. п. ф., если каждому ε > 0 соответствует достаточно однородное множество чисел [т. н. (B^p, ε) - почти периодов функции f(x)]: ... < τ_{- 2} < τ_{- 1} < τ₀ < τ₁ <...

такое, что для каждого i

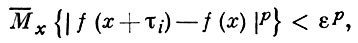
и для каждого с > 0

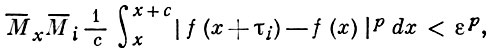
где

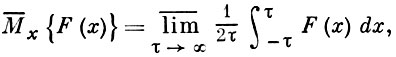
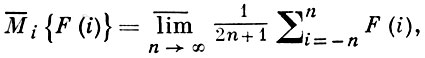
F(х) - действительная функция, определенная, соответственно, для действительного переменного и натурального аргумента.

Лит. : [1] Веsiсоvitсh A. S., «Рrос. London Math. Soc. », 1927, v. 27, p. 495-512; [2] eго же, там же, 1927, v. 26, р. 25-34; [3] Левитан Б. М., Почти периодические функции, М., 1953.

Е. А. Бредихина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.