БЕЗГРАНИЧНО ДЕЛИМЫХ РАСПРЕДЕЛЕНИЙ РАЗЛОЖЕНИЕ

Расстановка ударений: БЕЗГРАНИ`ЧНО ДЕЛИ`МЫХ РАСПРЕДЕЛЕ`НИЙ РАЗЛОЖЕ`НИЕ

БЕЗГРАНИЧНО ДЕЛИМЫХ РАСПРЕДЕЛЕНИЙ РАЗЛОЖЕНИЕ - представление безгранично делимых распределений в виде композиции (свертки) нек-рых распределений вероятностей. Распределения, участвующие в Б. д. р. р., наз. компонентами разложения.

Нек-рые Б. д. р. р. могут иметь компоненты, к-рые не являются безгранично делимыми распределениями (см. [1]). Важная задача теории Б. д. p. p. - описание класса I₀ безгранично делимых распределений, имеющих только безгранично делимые компоненты. Представители класса I₀ : нормальное распределение, Пуассона распределение, их композиция (см. Леви-Крамера теорема).

В исследованиях по проблеме описания класса I₀ важную роль играет введенный Ю. В. Линником [2] класс 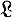безгранично делимых распределений, у к-рых функция G(x) в каноническом представлении Леви-Хинчина является функцией скачков с точками роста среди 0, μ_{m, 1}, μ_{m, 2}, m = 0, ±1, ±2, ..., где μ_{m, 1} > 0, μ_{m, 2} < 0 и числа μ_{m + 1, r} /μ_{m, r} (r = 1, 2; m = 0; ±1, ±2,...) - натуральные, отличные от 1. Если безгранично делимое распределение таково, что G( + 0) - G(- 0) > 0, то для его принадлежности к I₀ необходимо, чтобы оно принадлежало к 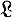. Достаточным это условие не является, но известно, что распределение класса 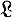принадлежит I₀, если

∫_{|x| > y} dG(x) = O(exp{ - ky²}),

при нек-ром k > 0 и при у → ∞.

Если G( + 0) - G(- 0) = 0, то принадлежность к 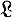не является необходимым условием принадлежности к I₀ . Так, напр., к I₀ принадлежат все безгранично делимые распределения, у к-рых функция G(x) постоянна при х < а и х > b, где 0 < а < b ≤ 2а.

Простое достаточное условие того, чтобы безгранично делимое распределение не принадлежало к I₀, состоит в следующем: на интервале а < х < b, где 0 < а < 2а < b, выполняется неравенство G'(x) ≥ const > 0. Из этого условия вытекает, что все устойчивые распределения, кроме нормального и единичного, а также гамма-распределение и χ² - распределение, не принадлежат к I₀ .

Класс I₀ является плотным в классе всех безгранично делимых распределений в топологии слабой сходимости, всякое безгранично делимое распределение представляется в виде композиции конечного или счетного множества распределений из I₀ .

Лит. : [1] Xинчин А. Я., «Бюлл. МГУ, секц. А», 1937, т. 1, в. 1, с. 6-17; [2] Линник Ю. В., «Теория вероятн. и её примен. », 1958, т. 3, с. 3-40; [3] его же, Разложения вероятностных законов, Л., 1960; [4] Линник Ю. В., Островский И. В., Разложения случайных величин и векторов, М., 1972; [5] Ramасhandran В., Advanced theory of characteristic functions, Calcutta, 1967; [6] Lukas E., Characteristic functions, L., 1970; [7] Лившиц Л. 3., Островский И. В., Чистяков Г. П., в сб. : Итоги науки и техники. Теория вероятностей. Математическая статистика. Теоретическая кибернетика, [т. 12], М., 1975, с. 5-42.

И. В. Островский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.