БЕГУЩЕЙ ВОЛНЫ МЕТОД

Расстановка ударений: БЕГУ`ЩЕЙ ВОЛНЫ` МЕ`ТОД

БЕГУЩЕЙ ВОЛНЫ МЕТОД - один из прямых методов численного решения задач вариационного исчисления. Применяется для решения задач оптимального управления невысокой размерности, но со сложными ограничениями на фазовые координаты и управляющие функции. После дискретизации функционала и системы дифференциальных уравнений исходная задача сводится к минимизации функционала:

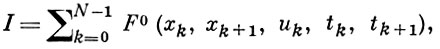
(1)

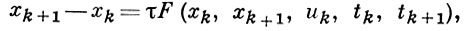
(2)

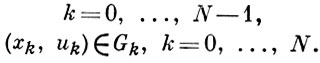
(3)

Здесь x_k, u_k - векторы фазовых координат n управлений в узле t_k (имеющие размерности соответственно n и m), причем u_k считается постоянным на каждом интервале (t_k, t_{k + 1}), G_k - заданные области (n + m)-мерного пространства (G₀ и G_N описывают граничные условия), τ = (Т - t₀)/N - шаг разбиения исходного интервала T - t₀ .

Б. в. м. применяется в случае n ≥ m, характерном для практич. задач и для к-рого использование других методов, основанных на варьировании в пространстве состояний (блуждающей трубки метод, локальных вариаций метод), осложнено в связи с трудоемкостью построения функции управления.

Заданное начальное приближение 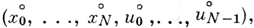, удовлетворяющее (2) и (3), улучшается в смысле критерия (1) на каждом участке от t_k до t_{k + p} (х_k, x_{k + p} - фиксируются), и этот участок последовательно сдвигается на один узел от начала траектории до конца, и обратно (отсюда название - «бегущая волна»).

Для каждой волны получается задача нелинейного программирования - минимизация

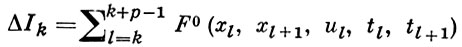
(4)

с р связями типа равенства (2) и условиями (3). При практич. реализации Б. в. м. вместо решения задачи (4) даются приращения ±h_i каждому из r свободных параметров и в случае уменьшения Δ I_k (4) и удовлетворения условий (3) получается новая траектория. Если траектория не меняется при полном проходе волны, то h_i дробятся.

При m = n Б. в. м. переходит в метод локальных вариаций.

Лит. : [1] Моисеев Н. Н., Элементы теории оптимальных систем, М., 1975; [2] Ватель И. А., Кононенко А. Ф., «Ж. вычисл. матем. и матем. физ. », 1970, т. 10, № 1, с. 67-73; [3] их же, Алгоритмы и программы (Информационный бюллетень), М., 1972, № 2, с. 7.

И. Б. Вапнярский, И. А. Ватель.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.