БАРЬЕР

Расстановка ударений: БАРЬЕ`Р

БАРЬЕР, барьер Лебега, в теории потенциала - функция, существование к-рой является необходимым и достаточным условием регулярности граничной точки в отношении поведения обобщенного решения задачи Дирихле в этой точке (см. также Перрона метод, Регулярная точка).

Пусть D - область в евклидовом пространстве ℝⁿ б n ≥ 2, и ξ - точка ее границы Г = ∂D. Барьером для точки ξ наз. всякая функция w_ξ (х), непрерывная в пересечении (D ∪ T) ∩ B замкнутой области D ∪ T и нек-рого шара B = B(R, ξ) с центром в точке ξ, супергармоническая внутри D ∩ B и положительная в (D ∪ Г) ∩ В, за исключением точки ξ, в к-рой она обращается в нуль. Напр., при n ≥ 3 во всякой граничной точке ξ, для к-рой существует замкнутый шар B¯ (R, y), имеющий с D ∪ Г единственную общую точку ξ, в качестве Б. можно взять гармонич. функцию

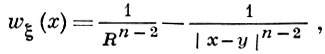
где R - радиус шара B(R, y), а y - его центр.

Б. в теории функций комплексного переменного - функция, из существования к-рой для всех гранияных точек области D следует, что D является голоморфности областью. Пусть D - область в комплексном пространстве ℂⁿ, n > 1, и ξ - точка границы T = ∂D. Б. в точке ξ есть всякая аналитич. функция f(z) в D, имеющая особенность в ξ. Так, для граничной точки ξ любой плоской области D ⊂ ℂ ' Б. является функция 1/(z - ξ). В каждой точке ξ = (ξ₁, ξ₂, ..., ξ_n) границы шара

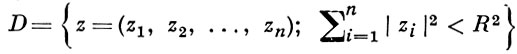
также существует Б. - функция 1/(ξ¯₁ z₁ + ... + ξ¯_n z_n - R²).

Б. существует в граничной точке ξ области D, если в D определена аналитич. функция f(z), неограниченная в ξ, т. е. такая, что для нек-рой последовательности точек {z^(k)} ⊂ D, сходящейся к ξ, имеем

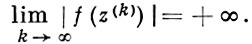
Обратное справедливо для областей D ⊂ ℂⁿ в следующей усиленной форме: для любого множества Е точек границы области D, в к-рых существует Б., найдется голоморфная в D функция, неограниченная во всех точках Е. Если Е всюду плотно на границе D, то D - область голоморфности.

Лит. : [1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964, гл. 4; [2] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [3] Шабат Б. В., Введение в комплексный анализ, ч. 2, 2 изд., М., 1976.

Е. Д. Соломенцев, М. Ширинбеков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.