
БАНАХОВО ПРОСТРАНСТВО
Расстановка ударений: БАНА`ХОВО ПРОСТРА`НСТВО
БАНАХОВО ПРОСТРАНСТВО, B-пространство, - полное нормированное векторное пространство. Исходными для создания теории Б. п. послужили введенные (в 1904-18) Д. Гильбертом (D. Hilbert), М. Фреше (М. Frechet) и Ф. Рисом (F. Riesz) функциональные пространства. Именно в этих пространствах были первоначально исследованы фундаментальные понятия сильной и слабой сходимости, компактности, линейного функционала, линейного оператора и др. Б. п. названы по имени С. Банаха, к-рый в 1922 (см. [1]) начал систематич. изучение этих пространств на основе введенной им аксиоматики и получил глубокие результаты.
Теория Б. п. развивалась параллельно с общей теорией линейных топологических пространств. Эти теории взаимно обогащались идеями и фактами. Так, идея полунормы, заимствованная из теории нормированных пространств, стала необходимым инструментом для построения теории локально выпуклых линейных топологич. пространств. Понятие слабой сходимости элементов и линейных функционалов в Б. п. обрело законченную форму в понятии слабой топологии. Теория Б. п. представляет собой хорошо разработанную область функционального анализа, имеющую (непосредственно или через теорию операторов) многочисленные применения в различных разделах математики.
Проблематика Б. п. складывается из нескольких направлений: геометрия единичной сферы, геометрия подпространств, линейно топологич. классификация, ряды и последовательности в Б. п., наилучшие приближения в Б. п., функции со значениями в Б. п. и др. Относительно теории операторов в Б. п. следует отметить, что многие ее предложения имеют непосредственное отношение к геометрии и топологии Б. п.
Примеры. Встречающиеся в математич. анализе Б. п. - это чаще всего множества функций или числовых последовательностей, подчиненные нек-рым условиям.
1) lp, р ≥ 1, - пространство числовых последовательностей x = {ξn}, для к-рых
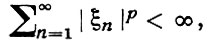
с нормой
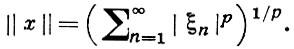
2) m - пространство ограниченных числовых последовательностей с нормой
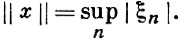
3) с - пространство сходящихся числовых последовательностей с нормой
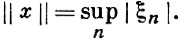
4) с0 - пространство сходящихся к нулю числовых последовательностей с нормой
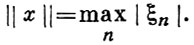
5) С [а, b] - пространство непрерывных на [а, b] функций x = x(t) с нормой
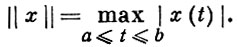
6) С [К] - пространство непрерывных функций на компакте К с нормой
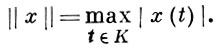
7) Сn [а, b] - пространство функций, имеющих непрерывные производные до порядка n включительно, с нормой
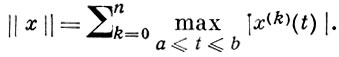
8) Сn [Im ] - пространство всех непрерывно дифференцируемых до порядка n функций, определенных в m-мерном кубе, с равномерной нормой по всем производным порядка не выше п.
9) М[а, b] - пространство ограниченных измеримых функций с нормой
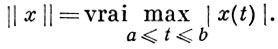
10) A (D) - пространство функций, аналитических в открытом единичном круге D и непрерывных в замкнутом круге D¯, с нормой
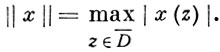
11) Lp (S; Σ, μ), р ≥ 1, - пространство функций x(s) на множестве S с вполне аддитивной мерой μ и с нормой
||x|| = (∫S |p x(s)|μ (ds))1/p .
12) Lp [a, b], p ≥ 1, - частный случай пространства Lp (S; Σ, μ) - пространство измеримых по Лебегу функций, суммируемых со степенью р, с нормой
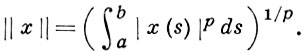
13) АР - пространство Бора почти периодич. функций с нормой
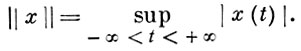
Пространства С [a, b], Сn [а, b], Lp [a, b], с, lp сепарабельны; пространства М [а, b], тm, АР несепарабельны; С [K] сепарабельно в том и только в том случае, если К-метрический компакт.
Подпространство Y Б. п., рассматриваемое отдельно от вмещающего пространства А, есть Б. п. Факторопространство X/Y нормированного пространства по подпространству Y становится нормированным пространством, если норму определить так: пусть Y1 = х1 + Y - класс смежности. Тогда
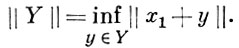
Если X - Б. п., то X/Y - тоже Б. п. Множество всех линейных функционалов, определенных в нормированном пространстве X, с нормой
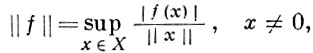
наз. пространством, сопряженным с X, и обозначается X*. Оно является Б. п.
Для Б. п. справедлива Хана-Банаха теорема о продолжении линейных функционалов: если линейный функционал определен на подпространстве Y нормированного пространства X, то его можно распространить с сохранением линейности и непрерывности на все пространство X. Более того, при этом можно обеспечить сохранение нормы расширенного функционала:
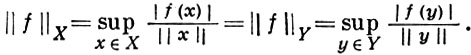
Справедливо и более общее утверждение: пусть действительная функция р(х), определенная в линейном пространстве, удовлетворяет условиям:
p(х + y) ≤ p(x) + p(y), р(λ х) = λ р(х), λ ≥ 0, х, у ∈ Х,
и пусть f(x) - действительный линейный функционал, определенный на подпространстве Y ⊂ X и такой, что
f(x) ≤ p(x), x ∈ Y.
Тогда существует линейный функционал F(x), определенный на всем X и такой, что
F(x) = f(x) для х ∈ Y; F(x) ≤ р(х) для х ∈ Y.
Следствием теоремы Хана-Банаха является «обратная» формула, связывающая нормы X и X*:
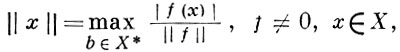
причем max в этой формуле достигается на нек-ром f = fx ∈ X*. Другое важное следствие - наличие достаточного множества непрерывных линейных функционалов. Говорят, что в Б. п. X существует достаточно много непрерывных линейных функционалов, если для любых х1 ≠ х2 ∈ X имеется такой определенный на X линейный функционал f, что f(x1) ≠ f(x2).
Для многих конкретных Б. п. известен общий вид линейного функционала. Так, в Lp [a, b], (р > 1) каждый линейный функционал определяется по формуле:
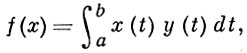
где y ∈ Lq [a, b], 1/p + 1/q = 1, а каждая функция y(t) ∈ Lq определяет по этой формуле линейный функционал f, причем
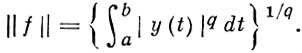
Таким образом, пространством, сопряженным с Lp, является Lq : L*p = Lq . В L1 [a, b] линейные функционалы задаются той же формулой, но в этом случае у ∈ М, так что L*1 = M.
Пространство X**, сопряженное с X*, наз. вторым сопряженным. Аналогично определяются третье, четвертое и т. д. сопряженные пространства. Каждый элемент из X может быть отождествлен с нек-рым линейным функционалом, определенным на X*:
F(f) = f(х), ∀ f ∈ X* (F ∈ X**, х ∈ Х).
При этом ||F|| = ||x||. Тогда можно считать X подпространством пространства X** и X ⊂ X** ⊂ XIV ..., X* ⊂ X*** ⊂.... Если при указанном вложении Б. п. совпадает со своим вторым сопряженным, то оно наз. рефлексивным. В этом случае все включения оказываются равенствами. Если же X не рефлексивно, то среди включений нет ни одного равенства. Если факторпространство X**/X имеет конечную размерность n, то X наз. квазирефлексивным порядка n. Квазирефлексивные пространства существуют для любого n.
Критерии рефлексивности Б. п. 1) X рефлексивно тогда и только тогда, когда для каждого f ∈ X* найдется х ∈ Х, на к-ром достигается sup в формуле
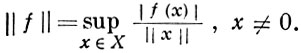
2) В рефлексивных Б. п., и только в них, каждое ограниченное множество компактно относительно слабой сходимости: любая его бесконечная часть содержит слабо сходящуюся подпоследовательность (теорема Эберлейна-Шмульяна). Пространства Lp и lp, р > 1, рефлексивны. Пространства L1, l1, С, М, с, m, АР нерефлексивны.
Б. п. наз. слабо полным, если в нем каждая слабо сходящаяся в себе последовательность слабо сходится к элементу пространства. Каждое рефлексивное пространство слабо полно. Кроме того, слабо полны Б. п. L1 и l1 . Еще более широкий класс - Б. п., не содержащие подпространств, изоморфных с0 . Эти пространства во многом подобны слабо полным.
Б. п. наз. строго нормированным, если его единичная сфера S не содержит отрезков. Для количественной оценки выпуклости единичного шара вводятся модули выпуклости: локальный модуль выпуклости 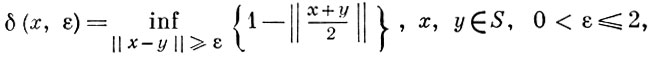 и равномерный модуль выпуклости
и равномерный модуль выпуклости
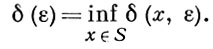
Если δ (х, ε) > 0 для всех х ∈ X и всех ε > 0, то Б. п. наз. локально равномерно выпуклым. Если δ (ε) > 0, то пространство наз. равномерно выпуклым. Каждое равномерно выпуклое Б. п. локально равномерно выпукло; каждое локально равномерно выпуклое Б. п. строго нормировано. В конечномерных Б. п. верны и обратные включения. Если Б. п. равномерно выпукло, то оно рефлексивно.
Б. п. наз. гладким, если для любых линейно независимых элементов х и у функция ψ (t) = ||x + ty|| дифференцируема при всех t. Б. п. наз. равномерно гладким, если для его модуля гладкости
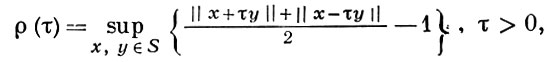
выполняется условие
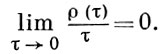
В равномерно гладких Б. п., и только в них, норма равномерно дифференцируема по Фреше. Равномерно гладкое Б. п. гладко. Обратное верно, если Б. п. конечномерно, Б. п. X равномерно выпукло (равномерно гладко) в том и только в том случае, если X* равномерно гладко (равномерно выпукло). Между модулем выпуклости Б. п. А и модулем гладкости X* существует связь
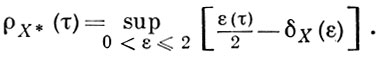
Если Б. п. равномерно выпукло (равномерно гладко), то таковы любое его подпространство и факторпространство. Б. п. Lp и lp (р > 1) равномерно выпуклы и равномерно гладки, причем
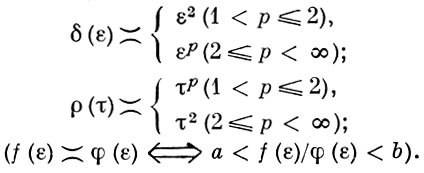
Б. п. М, С. A, L1, АР, m, с, l1 не являются строго нормированными и не являются гладкими.
В Б. п. справедливы следующие важные теоремы для линейных операторов:
Теорема Банаха-Штейнхауз а. Если семейство линейных операторов 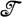 = {Тα} ограничено в каждой точке:
= {Тα} ограничено в каждой точке:
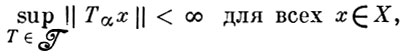
то оно ограничено по норме:
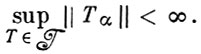
Теорема Банаха об обратном операторе. Если линейный непрерывный оператор отображает взаимно однозначно Б. п. X на Б. п. Y, то обратный оператор Т- 1 тоже непрерывен.
Теорема о замкнутом графике. Если замкнутый линейный оператор отображает Б. п. X в Б. п. Y, то он непрерывен.
Изометрия Б. п. сравнительно редкое явление. Классич. пример - Б. п. L2 и l2 . Б. п. С[K1 и С[К2 ] изометричны в том и только в том случае, если K1 и K2 гомеоморфны (теорема Банаха-Стоуна). Для изоморфных Б. п. мерой близости служит число
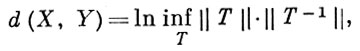
где Т пробегает всевозможные операторы, осуществляющие изоморфизм между X и Y. Если X изометрично Y, то d(X, Y) = 0. Однако существуют и не изометричные пространства, для к-рых d(X, Y) = 0; их наз. почти изометричными. Свойства Б. п., сохраняющиеся при изоморфизме, наз. линейно топологическими. К ним относятся сепарабельность, рефлексивность, слабая полнота. Изоморфная классификация Б. п. содержит, в частности, следующие утверждения:
Lr ≠ Ls ; lr ≠ ls, r ≠ s;
Lr ≠ ls, r ≠ s или r = s = 2;
M = m; С [0, 1] ≠ A(D);
С [K] = С [0, 1], если К-метрич. компакт мощности континуума;
Сn [Im ] ≠ С[0, 1].
Каждое сепарабельное Б. п. изоморфно локально равномерно выпуклому. Неизвестно (1977), каждое ли Б. п. изоморфно своей гиперплоскости. Существует Б. п., не изоморфное строго нормированному.
Отвлекаясь от линейной природы нормированных пространств, можно рассматривать их топология, классификацию. Два пространства гомеоморфны, если между их элементами может быть установлено взаимно однозначное и взаимно непрерывное (не обязательно линейное) соответствие. Неполное нормированное пространство не гомеоморфно никакому Б. п. Все бесконечномерные сепарабельные Б. п. гомеоморфны.
Универсальными (см. Универсальное пространство) в классе сепарабельных Б. п. являются С [0, 1] и A (D). В классе рефлексивных сепарабельных Б. п. нет даже изоморфно универсального. Б. п. l1 универсально в несколько ином смысле: каждое сепарабельное Б. п. изометрично нек-рому его факторпространству.
В каждом из перечисленных выше Б. п., кроме L2 и l2, существуют подпространства без дополнения. В частности, в m и М не дополняемо каждое бесконечномерное сепарабельное подпространство, в С [0, 1] не дополняемо каждое бесконечномерное рефлексивное подпространство. Если в Б. п. все подпространства дополняемы, то оно изоморфно гильбертову пространству. Неизвестно (1977), каждое ли Б. п. есть прямая сумма каких-то двух бесконечномерных подпространств. Подпространство Y дополняемо в том и только в том случае, если существует проектор, отображающий X на Y. Относительной проекционной константой λ (Y, X) подпространства Y в X наз. нижняя грань норм проекторов на Y. Каждое n-мерное подпространство Б. п. дополняемо и λ (Yn, X) ≤ √n Абсолютной проекционной константой λ (Y) Б. п. Y наз.
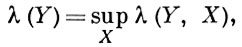
где X пробегает все Б. п., содержащие Y в качестве подпространства. Для любого бесконечномерного сепарабельного Б. п. Y имеем λ (Y) = ∞. Б. п., для к-рых λ (Y) ≤ λ < ∞, образуют класс 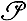 λ (λ ≥ 1). Класс
λ (λ ≥ 1). Класс 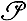 1 совпадает с классом пространств C(Q), где Q-экстремально несвязные компакты (см. Экстремально несвязные пространства).
1 совпадает с классом пространств C(Q), где Q-экстремально несвязные компакты (см. Экстремально несвязные пространства).
Основные теоремы о конечномерных Б. п. 1) Конечномерное нормированное пространство (Минковского пространство) полно, т. е. является Б. п. 2) Каждый линейный оператор в конечномерном Б. п. непрерывен. 3) Конечномерное Б. п. рефлексивно (размерность X* равна размерности X). 4) Б. п. конечномерно в том и только в том случае, если его единичный шар компактен. 5) Все n-мерные Б. п. попарно изоморфны; их множество становится компактом, если ввести расстояние
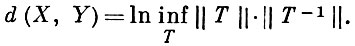
Ряд
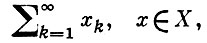
(*)
наз. сходящимся, если существует предел S последовательности частных сумм:
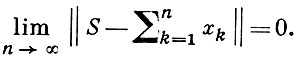
Если
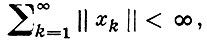
то ряд (*) сходится; в этом случае он наз. абсолютно сходящимся. Ряд наз. безусловно сходящимся, если он сходится при любой перестановке его членов. Сумма безусловно сходящегося ряда не зависит от порядка его членов. Для рядов в конечномерном пространстве (и, в частности, для числовых рядов) безусловная сходимость эквивалентна абсолютной. В бесконечномерных Б. п. из абсолютной сходимости следует безусловная, но обратное неверно ни в одном бесконечномерном Б. п. Последнее есть следствие теоремы Дворецкого-Роджерса: каковы бы ни были числа аk ≥ 0, подчиненные условию Σ а2k < ∞, в любом бесконечномерном Б. п. существует такой безусловно сходящийся ряд Σ xk, что ||xk || = ak, k = 1, 2,.... В пространстве с0 (а значит, и в любом Б. п., содержащем подпространство, изоморфное с0) для любой сходящейся к нулю последовательности аk ≥ 0 существует безусловно сходящийся ряд Σ xk, ||xk || = ak . В Lp (S, Σ, μ) из безусловной сходимости ряда Σ xk следует, что
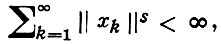
где
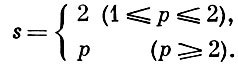
В равномерно выпуклом Б. п. с. модулем выпуклости Ϊ (Ϋ) из безусловной сходимости ряда Σ xk следует, что
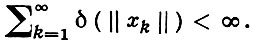
Ряд Σ xk наз. слабо абсолютно сходящимся, если для каждого сходится числовой ряд Σ |f(xk)|. Каждый слабо абсолютно сходящийся ряд в X сходится в том и только в том случае, если X не содержит подпространства, изоморфного с0 .
Последовательность элементов {еk}∞ Б. п. наз. минимальной, если любой ее член лежит вне замыкания X(n) = [ek ]k ≠ n линейной оболочки остальных членов. Последовательность наз. равномерно минимальной, если
ρ (еn ; Х(n) ≥ γ ||еn ||, 0 < γ ≤ 1, n = 1, 2,....
Если γ = 1, то последовательность наз. системой Ауэрбаха. В каждом n-мерном Б. п. существует полная система Ауэрбаха {еn)n1 . Неизвестно (1977), в каждом ли сепарабельном Б. п. существует полная система Ауэрбаха. Для каждой минимальной системы существует сопряженная система линейных функционалов {fn}, связанная с {ek} соотношениями биортогональности: fi (ei) = δij . В этом случае система {ek, fk} наз. биортогональной. Множество линейных функционалов наз. тотальным, если оно аннулирует только нулевой элемент пространства. В каждом сепарабельном Б. п. существует полная минимальная система с тотальной сопряженной. Каждый элемент х ∈ Х может быть формально разложен в ряд по биортогональной системе:
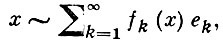
однако в общем случае этот ряд расходится.
Система элементов {ek}∞1 наз. базисом в X, если каждый элемент х ∈ Х может быть единственным обра зом представлен в виде сходящегося ряда
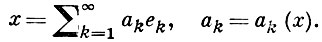
Каждый базис в Б. п. - полная равномерная минимальная система с тотальной сопряженной. Обратное неверно, как показывает пример системы {eint}∞- ∞, в С [0, 2π] и L1 [0, 2π].
Базис наз. безусловным, если каждая его перестановка - также базис, в противном случае базис наз. условным. Система {eint}∞- ∞ в Lp [0, 2π], р> > 1, р ≠ 2, - условный базис. Безусловным базисом в Lp, p > 1, является система Хаара. В пространствах С и L1 нет безусловного базиса. Неизвестно (1977), n каждом ли Б. п. есть бесконечномерное подпространство с безусловным базисом. Каждое Б. п. с безусловным базисом либо рефлексивно, либо содержит подпространство, изоморфное l1 или с0 .
Нормированные базисы {е'k} и {e''k} в Б. п. X1 и X2 наз. эквивалентными, если соответствие е'k ↔ е''k (k = 1, 2,...) может быть продолжено до изоморфизма между X1 и X2 . В каждом из пространств l2, l1, с0 каждый нормированный безусловный базис эквивалентен естественному базису. Базисы, построенные в важных для приложений Б. п., не всегда хорошо приспособлены к решению задач, напр. теории операторов. В связи с этим введены Т-базисы, или базисы суммирования. Пусть {tij}∞1 - матрица регулярного метода суммирования. Система элементов {еn} ⊂ X наз. Т-базисом, соответствующим данному методу суммирования, если каждый х ∈ X единственным образом представляется в виде ряда
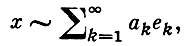
суммируемого этим методом к х. Тригонометрич. система {eint}∞- ∞ в С [0, 2π] - базис суммирования для методов Чезаро и Абеля. Каждый T-базис - полная минимальная (не обязательно равномерно) система с тотальной сопряженной. Обратное неверно. До недавнего времени (70-е гг.) одной из основных проблем теории Б. п. была восходящая к С. Банаху проблема базиса: в каждом ли сепарабельном Б. п. существует базис? Оставались открытыми также вопросы существования базиса в конкретных Б. п. Первый пример сепарабельного Б. п. без базиса построен в 1972; построены базисы в пространствах Cn (Im) и A(D).
Лит. : [1] Ваnасh S., «Fund. math. », 1922, t. 3, p. 133-81; [2] Банах С. С., Курс функцiонального аналiзу, Киiв, 1948; [3] Данфорд Н., Шварц Дж. Т., Линейные операторы. Общая теория, пер. с англ., М., 1962; [4] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961; [5] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959.
М. И. Кадец, Б. М. Левитан.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'