БАНАХА-МАЗУРА ФУНКЦИОНАЛ

Расстановка ударений: БАНА`ХА-МА`ЗУРА ФУНКЦИОНА`Л

БАНАХА-МАЗУРА ФУНКЦИОНАЛ, Банаха-Мазура оператор, - концепция вычислимого функционала (оператора), предложенная С. Банахом (S. Banach) и С. Мазуром (см. [1]) и трактующая вычислимость функционала (оператора), действующего из множества М₁ в множество М₂, как его свойство переводить всякую вычислимую последовательность элементов М₁ в вычислимую последовательность элементов М₂ (см. Вычислимая функция).

Пусть R - множество всех одноместных общерекурсивных функций. Функционал Ф, определенный на R и принимающий натуральные значения, наз. вычислимым по Банаху-Мазуру, или Б.-М. ф., если для всякой двухместной общерекурсивной функции g существует общерекурсивная функция f такая, что

f(n) = Ф(g(n, m))

(здесь g рассматривается как функция от m при каждом фиксированном n). Всякий общерекурсивный функционал и всюду определенный эффективный функционал (см. Конструктивное метрическое пространство) являются Б.-М. ф. С другой стороны, был построен пример Б.-М. ф., не совпадающего ни с каким общерекурсивным, а следовательно, и ни с каким эффективным функционалами (см. [2]). Важнейшим свойством Б.-М. ф. является их непрерывность (см. [1]): значения таких функционалов на любой общерекурсивной функции определяются лишь конечным числом значений этой функции.

Вышеописанная концепция вычислимости распространяется на функции действительного переменного. Пусть С - множество вычислимых последовательностей вычислимых действительных чисел; каждая последовательность {a_k} ∈ C задается парой общерекурсивных функций f и g таких, что при всех n, k

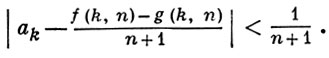
Функция действительного переменного φ наз. вычислимой по Банаху-Мазуру (множество таких функций обозначим 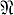), если для любой последовательности {а_k} из С последовательность {φ (a_k)} также принадлежит С. Каждая функция φ ∈ 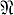непрерывна во всех вычислимых точках (см. [1]; таким образом, напр., sgn x ∉ 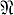. Вопрос о том, являются ли все функции из 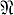вычислимо непрерывными, остается открытым (1977). Множество 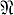оказывается замкнутым относительно ряда используемых в анализе операций, что позволяет успешно развивать на его базе вычислимый анализ (см. [1]).

Лит. : [1] Мazur S., Computable analysis, Warsz., 1963; [2] Friedberg R. M., «Bull. Acad. polon. sci. Sér. sci. math., astron. et phys. », 1958, t. 6, № 1, p. 1-5; [3] Mapков A. A., «Тр. Матем. ин-та. АН СССР», 1958, т. 52, с. 315-48; [4] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972.

Б. А. Кушнер.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.