БАНАХА ИНДИКАТРИСА

Расстановка ударений: БАНА`ХА ИНДИКАТРИ`СА

БАНАХА ИНДИКАТРИСА, функция кратности, непрерывной функции y = f(x), а ≤ x ≤ b, - целочисленная функция N(y, f), - ∞ < y < + ∞, равная числу корней уравнения f(x) = y. Если это уравнение при данном значений у имеет бесконечное множество корней, то

N(y, f) = + ∞,

а если оно не имеет корней, то

N(y, f) = 0.

Функция N (у, f) была определена С. Банахом [1] (см. также [2], с. 246). Он доказал, что для любой непрерывной на отрезке [а, b] функции f(x) ее индикатриса N (у, f) есть функция не выше 2-го класса Бэра, причем

(*)

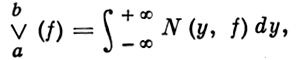
где 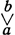(f) - вариация функции f(x) на отрезке [а, b]. Таким образом, равенство (*) можно принять за определение вариации непрерывной функции f(x). Б. и. определяют [с сохранением равенства (*)] и для функций, имеющих разрывы 1-го рода (см. [3]). Понятие Б. и. было использовано для определения вариаций функции нескольких переменных (см. [4], [5]).

Лит. : [1] Ваnасh S., «Fundam. math. », 1925, t. 7, p. 225-36; [2] Hатансон И. П., Теория функций вещественной переменной, 2 изд., М., 1957; [3] Лозинский С. М., «Вестн. Ленингр. ун-та», 1958, т. 7. Сер. Математика, механика, астрономия, № 2, с. 70-87; [4] Кронрод А. С., «Успехи матем. наук», 1950, т. 5, в. 1, с. 24-134; [5] Витушкин А. Г., О многомерных вариациях, М., 1955.

Б. И. Голубов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.