
БАЗИС
Расстановка ударений: БА`ЗИС
БАЗИС множества X - минимальное порождающее его подмножество В. Порождение означает, что применением операций нек-рого класса Ω к элементам b ∈ В получается любой элемент х ∈ Х. Это понятие связано с понятием зависимости: элементы X посредством операций из Ω ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество В' ∈ В не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент b ∈ В не порождается остальными его элементами. Напр., множество всех натуральных чисел ℤ0 имеет Б. единственный элемент 0 и порождается из него операцией ' непосредственного следования и ее итерациями; множество всех натуральных чисел > 1 порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов {1, i, j, k}, если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б. будет состоять лишь из трех элементов {1, i, j} (ибо k = ij).
Базис натурального ряда порядка k - подпоследовательность Ω множества ℤ0 натуральных чисел с включением 0, к-рая в результате k-кратного сложения с собой (операция порождения) дает все ℤ0 . Это означает, что каждое натуральное число n представимо в виде
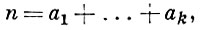
где ai ∈ Ω. Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б. ℤ0 порядка 4. Вообще, последовательность m-х степеней натуральных чисел является Б. ℤ0 (теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б. ℤ0 обобщается на случай произвольных числовых последовательностей, т. е. функций на ℤ0 .
Порождающие X множества существуют всегда (тривиально: X порождает X), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов Ω, содержащих бесконечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно Б. В определяется как параметризованное множество (или семейство), т. е. как функция b(t) на множестве индексов Т со значениями в X, причем b(Т) = В; мощность Т иногда наз. базисной размерностью (или рангом) X. Напр., счетное всюду плотное множество В сепарабельного топологич. пространства Р можно считать его Б. ; Р порождается из В операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже).
Базис топологии топологич. пространства X(база) - Б. 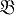 совокупности всех открытых подмножеств X; порождение осуществляется объединением элементов
совокупности всех открытых подмножеств X; порождение осуществляется объединением элементов 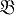 .
.
Базис булевой алгебры 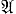 (двойственный базе
(двойственный базе 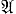 в смысле Тарского) - плотное множество (минимальной мощности) S в
в смысле Тарского) - плотное множество (минимальной мощности) S в 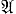 ; порождение
; порождение 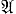 из S (а тем самым и само S) определяется условием s → a = ∨ (что равносильно s ⊂ a), где s ∈ S, a ∈
из S (а тем самым и само S) определяется условием s → a = ∨ (что равносильно s ⊂ a), где s ∈ S, a ∈ 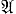 , ∨ - единица
, ∨ - единица 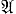 , « → » - операция импликации. Аналогично вводится и базис фильтра ∇ как множество S такое, что для любого a ∈ ∇ существует s ∈ S, и s ⊂ a.
, « → » - операция импликации. Аналогично вводится и базис фильтра ∇ как множество S такое, что для любого a ∈ ∇ существует s ∈ S, и s ⊂ a.
Большинство частных случаев Б. множества X вводится по следующей схеме. Пусть В(X) - булеан X, т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания) J называется отображение В(X) в себя такое, что: если А ⊂ В, то J(A) ⊂ J(В); A ⊂ J (А); JJ(A) = J(А).
Элемент х ∈ Х порождается множеством А, если x ∈ J(A); в частности, А порождает X, если J(А) = = X. Минимальное множество В, обладающее этим свойством, и наз. базисом X, определенным оператором J. Порождающий оператор J имеет конечный тип, если для любых А ⊂ Х, и х ∈ X из x ∈ J(A) следует x ∈ J(A0) для нек-рого конечного подмножества А0 ⊂ А; порождающий оператор J обладает свойством замещения, если для любых у, z ∈ X и А ⊂ Х из y ∉ J(A) и y ∈ J(A ∪ {z}) следует z ∈ J(A ∪ {y}). Порождающий оператор J конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение В(X) на два класса - зависимых и независимых множеств; множество А наз. зависимым, если у ∈ J(А\у) для нек-рого у ∈ А, и независимым, если y ∉ J(А\y) для любого у ∈ А. При этом А зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество А0 ⊂ А зависимо (независимо).
Для того чтобы множество В было Б. множества X, необходимо и достаточно, чтобы В было независимым порождающим X множеством или, иначе, максимальным независимым в X множеством.
Если А - произвольное независимое множество, а С - порождающее X множество, содержащее А, то существует Б. В в X такой, что А ⊂ В ⊂ С. В частности, X всегда обладает Б., и любые два его Б. равномощны.
В алгебраич. системах X важную роль играет понятие так наз. свободного базиса В, характеризующегося следующим свойством: произвольное отображение B ⊂ X в любую алгебраич. систему Y (той же сигнатуры) может быть продолжено до (гомо) морфизма X в Y, или, что то же самое, для любого (гомо)морфизма θ: Х → У и любого множества А ⊂ Х порождающие операторы JX и JY удовлетворяют условию:
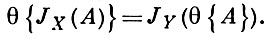
Алгебраич. система, имеющая свободный Б., наз. свободной.
Типичным примером является базис (унитарного) модуля M над кольцом K - свободное семейство элементов из М, порождающее М (см. [3]). Здесь семейство A = {at, t ∈ T) элементов K - модуля М наз. свободным, если из Σ ξt at = 0 (где ξt = 0 для всех, кроме конечного числа индексов t) следует ξt = 0 для всех t, а порождение осуществляется представлением элементов х в виде линейных комбинаций элементов at . существует (зависящее от х) множество элементов ξt ∈ К такое, что ξt = 0 для всех, кроме конечного числа индексов t, и имеет место разложение
x = ∑ ξt at
(т. е. X - линейная оболочка А). Б. M в этом смысле является его свободным Б. в вышеуказанном смысле; обратное также верно. Так, множество периодов двоякопериодич. функции f одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом ℤ), имеет свободный Б., наз. базисом периодов функции f; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных.
В случае, когда К - тело, всякий Б. (в прежнем смысле) является свободным. Напротив, существуют модули, не имеющие свободного Б. ; таковы, напр., неглавные идеалы в области целостности К, рассматриваемой как K - модуль.
Базис векторного пространства X над полем К - (свободный) Б. подлежащего X унитарного модуля. Аналогично, базис алгебры А над полем К - Б. подлежащего А векторного пространства. Все Б. данного векторного пространства X имеют одинаковую мощность, равную мощности Т, к-рая наз. его алгебраической размерностью. Каждый элемент х ∈ X представим линейной комбинацией элементов Б. единственным образом. Элементы ξt (x) ∈ K, являющиеся линейными функционалами на X, наз. компонентами (координатами) х в данном Б. {at}.
Множество А является Б. в X тогда и только тогда, когда А - максимальное (относительно включения) свободное множество в X.
Отображение
Ξ : x → ξx (t),
где ξx (t) = ξt (x), если ξt - значение t-й компоненты х в Б. А и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением X в пространство КT функций на Т со значениями в А. В данном случае образ Ξ (X) состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства X над полем K как биективное линейное отображение его на нек-рое подпространство К(Т) пространства КT функций на Т со значениями в K, где Т - нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на Т (напр., порядка) и структур на Т (напр., топологии) и согласованных с этим условий на К(Т) понятие обобщенного Б. практически мало полезно.
Иногда Б. векторного пространства X наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на X, даже если они и согласованы с его векторной структурой).
Базис Гамеля (Хамеля) - Б. поля действительных чисел ℝ, рассматриваемого как векторное пространство над полем рациональных чисел. Введен Г. Гамелем [4] для получения разрывного решения функционального уравнения f(x + y) = f(x) + f(у); график решения его всюду плотен на плоскости ℝ2 . Каждой почти периодич. функции f соответствует нек-рый счетный базис Гамеля β такой, что каждый показатель Фурье Λn этой функции принадлежит линейной оболочке β. При этом элементы β можно выбрать принадлежащими последовательности {Λi}; множество β наз. базисом почти периодической функции. Аналогичный Б. строится в кольце, содержащем тело Р и имеющем единицу тела Р своей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля.
Базис топологический (Б. топологического векторного пространства X над полем К) - семейство А = {at, t ∈ T} ⊂ X, свойства и функции к-рого аналогичны свойствам и функциям алгебраич. Б. векторного пространства. Понятие топологич. Б. - одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента х ∈ Х его разложение по Б. {at} и притом единственное, т. е. представление х в виде предела (в том или ином смысле) линейных комбинаций элементов at :
x = lim ∑ ξt (x)at,
где ξt (x) - линейные функционалы на X со значениями в К, наз. компонентами x в Б. A, или коэффициентами разложения x по Б. А. Очевидно, для существования разложения любого х необходимо, чтобы А было полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент X имел все компоненты равными нулю) необходимо, чтобы А было топологическим свободным множеством в X.
Смысл и практич. значение топологич. Б. (наз. далее просто Б.) заключается в установлении биективного линейного отображения X, наз. базисным отображением Ξ, на нек-рое, зависящее от X, пространство K(Т) функций со значениями в К, определенных на (топологическом) пространстве Т, а именно: Ξ (x): x ∈ X → ξx (t) ∈ K(T),
где ξx (t) = ξt (x), так что символически {ξt (X)} = К(Т) и {ξx (T)} = X; при этом строение К(Т) вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного X. Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность Т существенно уменьшается, одновременно упрощается и К(Т).
Пространство К (Т) содержит все конечнозначные функции, и множество элементов Б. {at} является биективным прообразом множества функций {ξt (s)}, имеющих лишь одно ненулевое значение, равное 1 («однозначных» функций):
at = Ξ- 1 [ξt (s)]
где ξt (s) = 1 при t = s и ξt (s) = 0 при t ≠ s. Другими словами, at - образующая одномерного подпространства At, дополнительного в X к гиперплоскости, определяемой уравнением ξt (x) = 0.
Таким образом, роль Б. {at} сводится к организации из множества компонент ξt (x), составляющих образ х при базисном отображении, суммируемого (в том или ином смысле) семейства {ξt (x)at}, т. е. Б. «разлагает» пространство X в (обобщенную) прямую сумму одномерных подпространств:
X = lim ∑ ξt (X)At
Аналогичным образом определяется Б. в векторных пространствах, наделенных равномерной, предельной (псевдотопологической), линейной (L-), близостной и другими дополнительными структурами.
Мыслимы (и существуют) обобщения понятия Б., идущие в различных направлениях. Так, введение топологии и меры на Т приводит к понятию так наз. непрерывной суммы элементов из X и соответствующим интегральным представлениям; разложение пространства X на необязательно одномерные компоненты находит применение в спектральной теории линейных операторов; рассмотрение вместо К(Т) произвольных топологич. алгебр над полем К (напр., алгебры мер на Т со значениями в К или даже в X, алгебры проекторов и т. д.) позволяет конкретизировать многие понятия абстрактной двойственности для топологич. векторных пространств и, в частности, использовать развитый аппарат теории характеров.
Базис счетный - наиболее исследованный (и в то же время практически наиболее важный) пример Б. - последовательность {аi} элементов пространства X такая, что каждому элементу х однозначно соответствует разложение его в ряд по Б. {аi}
∑ ξi (x)ai, ξi (x) ∈ K,
сходящийся (в топологии X) к х. Здесь ℤ, причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис] Так, напр., функции eikt, k ∈ ℤ образуют Б. в пространствах Lp, 1 < р < ∞ (абсолютно суммируемых в степени р периодич. функций), напротив, в пространствах L1, L∞ (измеримых функций, совпадающих почти всюду с ограниченными функциями) и С' (непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность X (напр., в. пространстве измеримых на отрезке [а, b] функций со значениями в ℝ счетного Б. быть не может). Впрочем, пространство l∞ ограниченных последовательностей, не будучи сепарабельным в топологии l∞, не обладает счетным Б., однако элементы аi = {δik} где δik = 1 при i = k и δik = 0 при i ≡ k, образуют Б. в слабой топологии σ (l∞, l1). Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7].
Счетный Б., однако, не всегда оказывается «достаточно хорошим» для применений (напр., компоненты ξi (x) не являются непрерывными, разложение х не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение.
Базис счетного типа - одно из обобщений понятия счетного Б., для к-рого хотя Т и несчетно, но разложение элемента х ∈ Х по нему естественно определяется: соответствующее пространство K(T) состоит из счетнозначных функций. Напр., полное ортонормированное множество {at} в гильбертовом пространстве Н является Б. ; если х ∈ Н, то ξt (x) = 〈 х, at 〉 (где 〈 ⋅, ⋅ 〉 - скалярное произведение в Н) для всех, за исключением быть может счетного множества, индексов t ∈ Т, и ряд Σ ξt at сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами at . Б. пространства АР всех комплекснозначных почти периодич. функций на ℝ состоит из функций еitλ ; здесь T = ℝ, К(Т) - совокупность счетнозначных функций, а базисное отображение определяется формулой
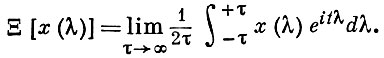
Базис безусловный - счетный Б. в пространстве X такой, что разложение любого элемента х сходится безусловно (т. е. сумма ряда не изменяется при перестановке любого числа его слагаемых). Так, напр., в пространствах с0 (последовательностей, сходящихся к нулю) и lp (последовательностей, суммируемых в степени р, 1 ≤ р < ∞) элементы аi = {δik} образуют безусловный Б. ; в пространстве С [а, b] непрерывных на отрезке [а, b] функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с0 (соответственно l1).
Б. {аi} и {bi} соответствующих банаховых пространств X и Y наз. эквивалентными, если существует биективное линейное отображение Т: аi → bi распространяемое до изоморфизма X в Y; эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства l1, l2, с0 обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении lp × lq (1 ≤ р < q < ∞) квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
Базис суммирующий - обобщение понятия безусловного Б., соответствующее множеству Т произвольной мощности и совпадающее с ним при Т = ℤ, - семейство А = {at, t ∈ T} такое, что для любого элемента х ∈ X существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х: для любой окрестности нуля U ⊂ X найдется конечное подмножество AU ⊂ А такое, что для каждого конечного множества А' ⊃ АU имеет место
(∑t ∈ A' ξt at - x) ∈ U,
т. е. когда частичные суммы образуют систему (фильтр) Коши. Так, напр., любой ортонормированный Б. гильбертова пространства является суммирующим Б. Аналогично определяется слабый суммирующий базис. Вполне суммирующий базис - такой суммирующий Б., что существует ограниченное множество В такое, что множество полунорм {pB (ξt at)} суммируемо. Вполне суммирующий Б. не более чем счетен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий.
Базис абсолютный (абсолютно суммирующий базис) - суммирующий Б. локально выпуклого пространства над нормированным полем такой, что для каждой окрестности нуля U и для каждого t ∈ T суммируемо семейство полунорм {рU (at)}. Всякий безусловный счетный Б. абсолютен, т. е. ряд Σ |ξi (x)|p(ai) сходится для всех х ∈ Х и всех непрерывных полунорм р(⋅). Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1 . Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13].
Базис Шаудера - Б. {at, t ∈ Т) пространства X такой, что определенное им базисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты ξt (x) для любого х ∈ X и, в частности, коэффициенты разложения х по этому Б., являются непрерывными функционалами на X. Определен впервые Ю. Шаудером [5] для случая T = ℤ Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б.
Базис Шаудера характеризуется тем, что {at} и {ξt} образуют биортогональную систему. Напр., в пространствах с0 и lp, р ≥ 1 последовательности ai = {δik} образуют счетный базис Шаудера. В пространстве С [а, b] счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него {ξt} будет Б. в сопряженном пространстве X*, и ограниченно полным, т. е. если ограниченность множества частных сумм ряда Σ ξi ai - влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в X нет подпространств, изоморфных l1 (соответственно с0).
Базис Шаудера в локально выпуклом пространстве равностепенно непрерывен, если для каждой окрестности нуля U найдется окрестность нуля V такая, что
|ξt |pU (at) ≤ pV (x)
для всех х ∈ Х, t ∈ T. Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.
Лит. : [1] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [2] Мальцев А. И., Алгебраические системы, М., 1970; [3] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [4] Hamel G., «Маth. Аnn. », 1905, Bd 60, S. 459-62; [5] Sсhаudеr J., «Маth. Z. », 1927, Bd 26, S. 47-65, 417-31; [6] Энфло П., «Математика», 1974, т. 18, № 1, с. 146-155; [7] Зобин Н. М., Митягин Б. С., «Функциональный анализ и его приложения», 1974, т. 8, № 4, с. 35-47; [8] Эдвардс Р. Э., Функциональный анализ, пер. с англ., М., 1969; [9] Diеudоnné J., «Аrсh. Маth. », 1951, Bd 1, S. 81-115; [10] Аrsоv М. G., «Расifiс J. Маth. », 1960, t. 10, р. 365-79; [11] Bessaga С. Pelczynski A., «Studia Маth. », 1960, v. 19, р. 53-62; [12] James R. С., «Аnn. Маth. », 1950, v. 52, № 2, р. 518-27; [13] Дынин А. С., Митягин Б. С., «Bull. Acad. Polon. Sci. », (Ser. Sci math.), 1960, t. 8, p. 535-40; [14] Дэй M. M., Нормированные линейные пространства, пер. с англ., М., 1961; [15] Пич А., Ядерные локально выпуклые пространства, пер. с нем., М., 1967.
М. И. Войцеховский, М. И. Кадец.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'