БАЗА

Расстановка ударений: БА`ЗА

БАЗА топологического пространства X (база топологии, базис топологии, открытая база) - семейство 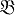открытых подмножеств X такое, что каждое открытое множество G ⊂ X является объединением элементов U ⊂ 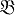. Понятие Б. - одно из основных в топологии: во многих вопросах, относящихся к открытым множествам нек-рого пространства, достаточно ограничиться рассмотрением элементов его Б. Пространство может иметь много Б., наибольшую из к-рых образует семейство всех открытых множеств. Минимум мощностей всех Б. наз. весом топологич. пространства X. В пространстве веса τ существует всюду плотное множество мощности ≥ τ. Пространства со счетной Б. наз. также пространствами со второй аксиомой счетности. Двойственное понятие замкнутой Б., образованной дополнениями к элементам Б., мало употребительно.

Локальной Б. пространства А в точке х ∈ X {базой точки х) наз. семейство 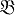(х) его открытых множеств, обладающее свойством: для любой окрестности Ох точки х найдется элемент V ∈ 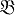(x) такой, что x ∈ V ⊂ Ox. Пространства, имеющие счетную локальную Б. в каждой точке, наз. также пространствами с первой аксиомой счетности. Семейство 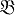открытых в X множеств является Б. тогда и только тогда, когда оно является локальной Б. каждой его точки х ∈ X.

Пусть m, n - нек-рые кардинальные числа. Б. 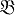пространства X наз. m-точечной, если каждая точка х ∈ Х принадлежит не более чем m элементам семейства 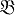, в частности, при m = 1 Б. наз. дизъюнктной, при конечном m-точечно конечной, при m = 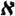₀ - точечно счетной. Б. 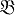пространства X наз. m - локальной, если для каждой точки х ∈ Х существует ее окрестность Ох, пересекающаяся с не более чем m элементами семейства 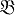; в частности, при m = 1 Б. наз. дискретной, при конечном m - локально конечной, при m = 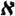₀ - локально счетной. Б. 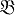наз. n - m - точечной (n - m - локальной), если она является объединением множества мощности nm - точечных (m - локальных) Б. ; таковы, напр., при n = 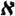₀ σ - дизъюнктные, σ - точечно конечные, σ - дискретные, σ - локально конечные Б.

Эти понятия находят применение главным образом в критериях метризуемости пространств. Так, пространство со счетной Б. или с первой аксиомой счетности и точечно счетной Б. метризуемо; регулярное пространство с σ - дискретной или с σ - локально конечной Б. метризуемо (обратное верно, однако, лишь для первого утверждения).

Б. 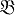пространства А наз. равномерной (k-равномерной), если для каждой точки х ∈ X (каждого бикомпактного подмножества F) и каждой ее (его) окрестности Ox (OF) лишь конечное число элементов Б. содержит х (пересекается с F) и одновременно пересекается с дополнением Х\Ох (X\OF). Пространство X метризуемо тогда и только тогда, когда оно является паракомпактом с равномерной Б. (колмогоровским, или Т₀ пространством с k-равномернои Б.).

Б. 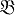пространства А наз. регулярной, если для каждой точки х ∈ Х и произвольной ее окрестности Ох существует такая окрестность О'х, что множество всех элементов Б., пересекающихся одновременно с О'х и Х\Ох, конечно. Для метризуемости достижимого или T₁ - пространства необходимо и достаточно наличие в нем регулярной Б.

Обобщением понятия Б. является так наз. π-база (решеточная Б.) - семейство 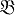открытых в пространстве X множеств такое, что каждое непустое открытое в X множество содержит непустое множество из 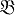, т. е. 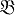плотно в X по Хаусдорфу. Всякая Б. является π-базой; обратное неверно, напр., в Стоуна-Чеха бикомпактном расширении в ℤ⁺ множества натуральных чисел множество ℤ⁺ образует лишь π-базу.

Лит. : [1] Александров П. С., Колмогоров А. Н., Введение в общую теорию множеств и функций, М. - Л., 1948; [2] Урысон П. С., Труды по топологии и другим областям математики, т. 1-2, М. - Л., 1951; [3] Александров И. С., Пасынков Б. А., Введение в теорию размерности, Введение в теорию топологических пространств и общую теорию размерности, М., 1973; [4] Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974; [5] Бурбаки Н., Общая топология Основные структуры, пер. с. франц., М., 1968.

А. А. Мальцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.