АФФИННОЕ АЛГЕБРАИЧЕСКОЕ МНОЖЕСТВО

Расстановка ударений: АФФИ`ННОЕ АЛГЕБРАИ`ЧЕСКОЕ МНО`ЖЕСТВО

АФФИННОЕ АЛГЕБРАИЧЕСКОЕ МНОЖЕСТВО, аффинное алгебраическое k-множество, - множество решений нек-рой системы алгебраич. уравнений. Пусть k поле и k¯ - его алгебраич. замыкание. Подмножество X декартова произведения k¯ⁿ наз. аффинным алгебраическим k-множеством, если его точки являются общими нулями нек-рого семейства S многочленов кольца k[Т] = k[T₁, ..., T_n ]. Множество 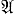_X всех многочленов из k[T₁, ..., T_n ], обращающихся в нуль на X, образует идеал, к-рый наз. идеалом аффинного алгебраического k-множества. Идеал 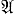_X совпадает с радикалом идеала I(S), порожденного семейством S, т. е. с множеством таких многочленов f ∈ k[T₁, ..., T_n ], что f^m ∈. I(S) для нек-рого натурального m. А. а. м. 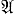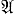X и Y совпадают тогда и только тогда, когда _X = _Y . А. а. м. X может быть задано системой образующих идеала 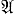_X . В частности, всякое А. а. м. может быть задано конечным числом многочленов (f₁, ..., f_k) ∈ k[T]. Равенства f₁ =... = f_k = 0 наз. уравнениями А. а. м. X. А. а. м. пространства k¯ⁿ образуют решетку относительно операций пересечения и объединения. При этом идеал пересечения X ∩ Y совпадает с суммой идеалов 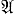_X + 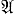_Y, а идеал объединения X ∪ Y - с пересечением идеалов 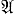_X ∪ 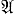_X . Все множество k¯ⁿ является А. а. м., к-рое наз. аффинным пространством над полем k и обозначается Aⁿ_k ; ему соответствует нулевой идеал. Пустое подмножество множества k¯ⁿ тоже есть А. а. м. с единичным идеалом. Факторкольцо k[Х] = k[Т]/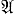_X наз. координатным кольцом А. а. м. X. Оно отождествляется с кольцом k-регулярных функций на X, т. е. с кольцом k¯-значных функций f : Х → k¯, для к-рых существует такой многочлен F ∈ k[Т], что f(x) = F(x) для всех х ∈ X. А. а. м. X наз. неприводимым, если оно не является объединением двух собственных аффинных алгебраич. подмножеств. Эквивалентное определение состоит в том, что идеал 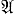_X должен быть простым. Неприводимые А. а. м. вместе с проективными алгебраич. множествами являлись объектами классической алгебраич. геометрии. Они наз. соответственно аффинными алгебраическими многообразиями и проективными алгебраическими многообразиями над полем k (или k-многообразиями). А. а. м. наделяются структурой топологич. пространства. Замкнутыми множествами этой топологии (Зариского топологии) являются неприводимые аффинные алгебраич. подмножества. А. а. м. неприводимо тогда и только тогда, когда оно неприводимо как топологич. пространство. Дальнейшее развитие понятия А. а. м. приводит к понятиям аффинного многообразия и аффинной схемы.

Лит. : [1] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [2] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972.

И. В. Долгачев, В. А. Исковских.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.