АФФИННАЯ СВЯЗНОСТЬ

Расстановка ударений: АФФИ`ННАЯ СВЯ`ЗНОСТЬ

АФФИННАЯ СВЯЗНОСТЬ - дифференциально-геометрическая структура на гладком многообразии М, специальный вид связности на многообразии, когда приклеенное к М гладкое расслоенное пространство Е имеет типовым слоем аффинное пространство A_n размерности n = dim М. Структурой такого Е к каждой точке х ∈ М присоединяется экземпляр аффинного пространства (А_n)_x, к-рый отождествляется с касательным центроаффинным пространством Т_x (М). А. с. предусматривает такое сопоставление каждой гладкой кривой L ∈ М с началом х₀ и каждой ее точке x_t аффинного отображения (A_n)_xt → (A_n)_x0, что удовлетворяется ниже сформулированное условие. Пусть М покрыто координатными областями, в каждой из к-рых фиксировано гладкое поле аффинного репера в (А_n)_x, у к-рого начало совпадает с х (т. е. фиксированы n гладких векторных полей, линейно независимых в каждой точке х области). Требуется, чтобы при t → 0, когда x_t перемещается по L до х₀, отображение (A_n)_xt → (A_n)_x0 стремилось к тождественному отображению, причем главная часть его отклонения от последнего определялось относительно некоторого из реперов системой линейных дифференциальных форм

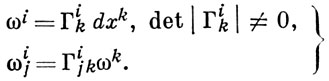
(1)

Итак, образом при (A_n)_xt → (A_n)_x0 репера в точке x_t является система из точки в (A_n)_x0 с радиус-вектором e_i [ωⁱ (X)t + εⁱ (t)] и n векторов e_i [δⁱ_j + ωⁱ_j (X)t + εⁱ (t)], где X - касательный вектор к L в точке х₀, причем

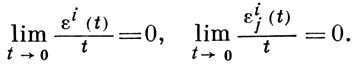
Многообразие М с заданной на ней А. с. наз. пространством аффинной связности. При преобразовании репера поля в произвольной точке x ∈ М согласно формулам e_i' = A_i'^j e_j, е_j = A_j^i' e_i', т. е. при переходе к произвольному элементу главного расслоенного пространства Р реперов в касательных пространствах (A_n)_x с началами в точке х, формы (1) заменяются следующими 1-формами на Р:

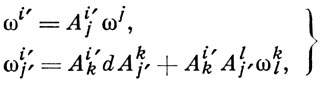
(2)

а 2-формы

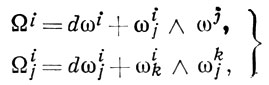
(3)

преобразуются так:

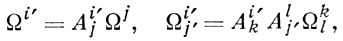
где Ω^i' и Ω_j' составлены согласно (3) из форм (2). Уравнения (3) называются структурными уравнен и я м и А. с. на М, где левые части - так наз. кручения формы Ωⁱ и кривизны формы Ω_jⁱ - полубазовы, т. е. являются линейными комбинациями ω^k ∧ ω^l :

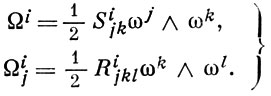
(4)

Любые 1-формы ωⁱ и ω_jⁱ, заданные на Р и удовлетворяющие уравнениям (3) с левыми частями вида (4), определяют нек-рую А. с. на М. Отображение (A_n)_xt → (A_n)_x0 для кривой L ∈ М получается следующим образом: нужно выбрать нек-рое гладкое поле репера в координатной окрестности начала х₀ кривой L, и образ репера в точке x_t определить как решение {x(t), e_i (t)} системы

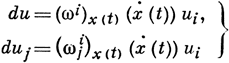
(5)

при начальных условиях u(0) = 0, u_i (0) = е_i, где хⁱ = xⁱ (t) - уравнения кривой L. Кривая, описываемая в (A_n)_x0 точкой с радиус-вектором x(t) относительно х₀, наз. разверткой кривой L. Поле репера в координатной окрестности можно выбрать так, чтобы ωⁱ = dxⁱ ; тогда ωⁱ_j = Гⁱ_jk dx^k . На пересечении координатных окрестностей 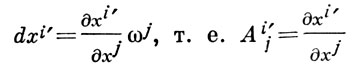и

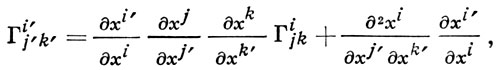
(6)

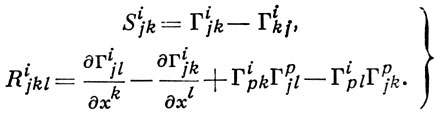
(7)

Здесь Sⁱ_jk и Rⁱ_jkl составляют, соответственно, кручения тензор и кривизны тензор А. с. на М. А. с. на М может быть задана системой функций Гⁱ_jk на каждой координатной окрестности, преобразующейся на пересечении окрестностей по формуле (5) - так наз. объектом А. с. Отображение (A_n)_xt → (A_n)_x0 получается с помощью системы (5), в к-рую следует подставить

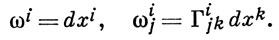
Если в нек-рой окрестности точки х₀ дано векторное поле X = ξⁱ e_i то при (A_n)_xt → (A_n)_x0 вектор X_x(t) отображается в вектор ξⁱ (x_t)e_i (t) (где {e_i {t)} - решение системы (5)), дифференциал к-рого в (A_n)_x0 при t = 0:

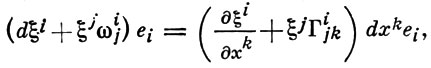
наз. ковариантным дифференциалом поля X относительно данной А. с. Здесь

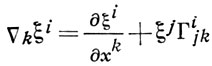
образуют тензорное поле, наз. ковариантной производной поля X = ξⁱ e_i . Если дано второе векторное поле Y = η^k e_k, то определяется ковариантная производная поля А в направлении Y:

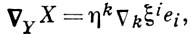
к-рая относительно произвольного поля репера может быть определена также формулой

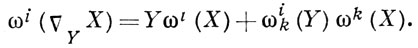
А. с. на М может быть задана и как билинейный оператор ∇, к-рый двум векторным ролям X, Y ставит в соответствие третье ∇_Y Х и обладает свойствами:

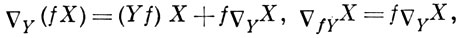
где f - гладкая функция на М. Связь с вышеуказанными способами задания устанавливается формулой: ∇_ek e_j = Гⁱ_jk e_i где {е_i} - поле репера; поля тензоров кручения и кривизны

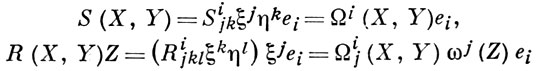
определяются формулами

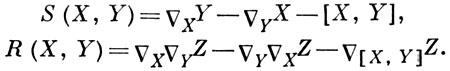
Векторное поле X наз. параллельным вдоль кривой L, если ∇_{ẋ (t)} X_x(t) = 0 тождественно относительно t, т. е. если вдоль L

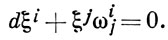
Параллельными векторными полями осуществляется параллельное перенесение векторов (и вообще тензоров) в А. с, представляющее собой линейное отображение касательных векторных пространств Т_xt (М) → Т_x0 (М), определяемые отображением (A_n)_xt → (A_n)_x0 . В этом смысле каждая А. с. порождает нек-рую линейную связность на М.

Кривая L наз. геодезической линией в данной А. с, если ее развертка является прямой линией; другими словами, если в подходящей параметризации ее касательное векторное поле x(t) параллельно вдоль ее. Относительно локальной координатной системы геодезич. линии определяются системой

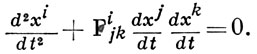
Через каждую точку в каждом направлении проходит одна геодезическая.

Существует взаимно однозначное соответствие между А. с. на М и связностями в главных расслоенных пространствах свободных аффинных реперов в (A_n)_x, х ∈ М, ими порождаемыми. Замкнутым кривым с началом и концом в х соответствуют аффинные преобразования (A_n)_x → (A_n)_x, к-рые образуют неоднородную голономии группу данной А. с. Соответствующие линейные автоморфизмы Т_x (М) → Т_x (М) образуют однородную группу голономии. Согласно теореме о голономии алгебры Ли этих групп определяются 2-формами кручения Ωⁱ и кривизны Ωⁱ_j . Для последних имеют место тождества Бианки:

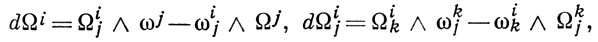
к-рые, в частности, для А. с. без кручения, когда Ωⁱ = 0, сводятся к следующим:

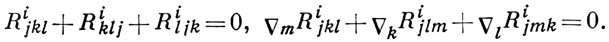
Понятие А. с. возникло в 1917 в римановой геометрии (в виде Леви-Чивита связности); самостоятельный смысл оно обрело в 1918-24 в работах Г. Вейля [1] и Э. Картана [2].

Лит. : [1] Weyl Н., Raum, Zeit, Materie, 5 Aufl., В., 1923; [2] Сartan E., «Аnn. scient. École norm. supér. », 1923, т. 40, p. 325-412; 1924, t. 41, p. 1-25; 1925, t. 42, p. 17-88; [3] Кapтан Э., Пространства аффинной, проективной и конформной связности, пер. с франц., Казань, 1962; [4] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [5] Постников М. М., Вариационная теория геодезических, М., 1965.

Ю. Г. Лумисте.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.