
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Расстановка ударений: АФФИ`ННАЯ ДИФФЕРЕНЦИА`ЛЬНАЯ ГЕОМЕ`ТРИЯ
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ - раздел геометрии, изучающий дифференциально-геометрич. свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства.
В эквиаффинной плоскости каждые два вектора a, b имеют инвариант (a, b ) - площадь параллелограмма, построенного на векторах a и b . С помощью этого понятия для кривой r = r (t), отличной от прямой, строится инвариантный параметр
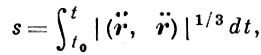
наз. эквиаффинной дугой. Дифференциальный инвариант
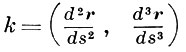
наз. эквиаффинной кривизной плоской кривой. Постоянство эквиаффинной кривизны характеризует кривые 2-го порядка. Натуральное уравнение k = f(s) определяет кривую с точностью до эквиаффинного преобразования. Вектор n = d2r /ds2 направлен по аффинной нормали к плоской кривой: аффинная нормаль в точке М, k ≠ 0, касается геометрич. места середин хорд кривой, параллельных касательной в точке М и совпадает с диаметром параболы, имеющей в точке М соприкосновение 3-го порядка с кривой.
При переходе к общей аффинной группе у кривой рассматривают два более сложных инварианта: аффинную дугу σ и аффинную кривизну א. Они могут быть выражены через введенные выше инварианты s и k:
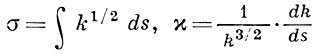
(в эквиаффинной геометрии сами величины s и k для краткости наз. аффинной дугой и аффинной кривизной). Подобным же образом строятся центроаффинная дуга, пентроаффинная кривизна, эквицентроаффинная дуга и эквицентроаффинная кривизна плоской кривой.
В эквиаффинной пространстве каждым трем векторам a, b, c может быть отнесен инвариант (a, b, c ) - объем ориентированного параллелепипеда, определяемого этими векторами. Натуральный параметр (эквиаффинная дуга) кривой r = r (t) (r ∈ С3) определяется формулой
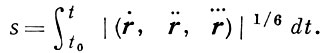
Дифференциальные инварианты x = (r ', r ''', rIV), τ = - (r '', r ''', rIV), где штрихи означают дифференцирование по натуральному параметру, наз. соответственно эквиаффинной кривизной и эквиаффинным кручением пространственной кривой. Изучение кривой сводится к выбору того или иного сопровождающего репера; особую роль играет репер, образованный векторами
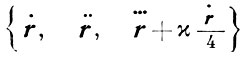
и определяемый дифференциальной окрестностью 4-го порядка рассматриваемой кривой. Разработана также центроаффинная теория пространственных кривых (см. [5]).
Для поверхности r = r (u1, u2) в эквиаффинном пространстве, отличной от развертывающейся поверхности, строится тензор
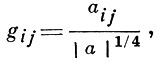
где aij = (r1, r2, rij, а = det(aij), ri = ∂ir, rij = ∂ijr . Вектор
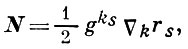
где ∇k - символ ковариантной производной в связности с метрич. тензором gij, задает направление аффинной нормали к поверхности. Аффинная нормаль проходит через центр соприкасающейся квадрики Ли. Деривационные уравнения
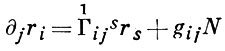
определяют внутреннюю связность 1-го рода 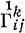 поверхности. Наряду с ней возникает внутренняя связность 2-го рода
поверхности. Наряду с ней возникает внутренняя связность 2-го рода 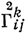 , определяемая деривационными уравнениями
, определяемая деривационными уравнениями
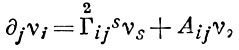
где ν - ковариантный вектор, определяющий касательную плоскость к поверхности и подчиненный условию нормировки Nν = 1. Связности 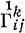 и
и 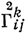 являются сопряженными относительно тензора gij в смысле А. П. Нордена (см. [3]). Тензор
являются сопряженными относительно тензора gij в смысле А. П. Нордена (см. [3]). Тензор
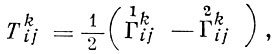
играющий также основную роль в проективной дифференциальной геометрии, позволяет построить симметрич. ковариантный тензор
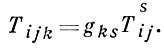
Строятся также две основные формы поверхности: квадратичная форма
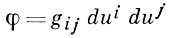
и кубическая форма Фубини-Пика
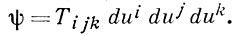
Эти формы связаны условием аполярности
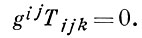
Две такие формы, удовлетворяющие дополнительным дифференциальным условиям, определяют поверхность с точностью до эквиаффинных преобразований. Все эти положения обобщаются на многомерный случай.
В аффинном и эквиаффинном пространствах выделяется много специфич. классов поверхностей: аффинные сферы (у к-рых аффинные нормали образуют связку), аффинные поверхности вращения (аффинные нормали пересекают одну собственную или несобственную прямую), аффинные минимальные поверхности и др.
Помимо кривых и поверхностей, изучаются также иные геометрич. образы эквиаффинного пространства, напр. конгруэнции и комплексы прямых, векторные поля и др.
Наряду с эквиаффинной дифференциальной геометрией разрабатывается дифференциальная геометрия общей аффинной группы и других ее подгрупп как в трехмерном, так и в многомерном пространствах (центроаффинном, эквицентроаффинном, аффинно-симплектическом, биаффинном и т. д.).
Лит. : [1] Blaschke W., Affine Differential géométrie, В., 1923; [2] Salkowski Е., Affine Differential géométrie. В. - Lpz., 1934; [3] Hоpдeн А. П., Пространства аффинной связности, М. - Л., 1950; [4] Итоги науки. Геометрия. 1963, М., 1965, с. 3-64; [5] Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959.
А. П. Широков.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'