
АССОЦИАТИВНОЕ ИСЧИСЛЕНИЕ
Расстановка ударений: АССОЦИАТИ`ВНОЕ ИСЧИСЛЕ`НИЕ
АССОЦИАТИВНОЕ ИСЧИСЛЕНИЕ - название, установившееся за исчислениями нек-рого точно охарактеризованного типа, хорошо приспособленными для задания конечно определенных ассоциативных систем (полугрупп). Термин «А. и. » введен А. А. Марковым. Им же было осуществлено построение развернутой теории А. и. (см. [2], гл. VI).
Всякое А. и.  определяется указанием нек-рого алфавита А и конечного списка σ соотношений в А - пар слов в этом алфавите. Слова, входящие в состав соотношений, обычно наз. их частями - левыми и правыми. Допустимым относительно σ действием над словами в А наз. любая подстановка одной из частей к.-л. соотношения, принадлежащего σ, вместо любого вхождения другой части того же соотношения. А. и.
определяется указанием нек-рого алфавита А и конечного списка σ соотношений в А - пар слов в этом алфавите. Слова, входящие в состав соотношений, обычно наз. их частями - левыми и правыми. Допустимым относительно σ действием над словами в А наз. любая подстановка одной из частей к.-л. соотношения, принадлежащего σ, вместо любого вхождения другой части того же соотношения. А. и.  представляет собой разрешение производить, исходя из любого слова Р в А, любые допустимые относительно σ действия. Обо всех словах Q, к-рые при этом получаются (в том числе и о самом исходном слове Р), говорят, что они эквивалентны Р в А. и.
представляет собой разрешение производить, исходя из любого слова Р в А, любые допустимые относительно σ действия. Обо всех словах Q, к-рые при этом получаются (в том числе и о самом исходном слове Р), говорят, что они эквивалентны Р в А. и.  (в символич. записи
(в символич. записи  : P
: P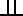 Q). Отношение
Q). Отношение 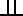 для любого А. и.
для любого А. и.  рефлексивно, симметрично и транзитивно. Кроме того, из
рефлексивно, симметрично и транзитивно. Кроме того, из  : P
: P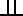 Q и
Q и  : R
: R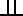 S следует, что
S следует, что  : PR
: PR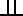 QS. Это позволяет естественным образом сопоставить всякому А. и.
QS. Это позволяет естественным образом сопоставить всякому А. и.  нек-рую конечно определенную ассоциативную систему K
нек-рую конечно определенную ассоциативную систему K , взяв в качестве ее элементов классы слов, эквивалентных друг другу в
, взяв в качестве ее элементов классы слов, эквивалентных друг другу в  , а в качестве операции умножения в K
, а в качестве операции умножения в K - операцию, естественно индуцируемую операцией, соединения слов в А. Так построенная ассоциативная система K
- операцию, естественно индуцируемую операцией, соединения слов в А. Так построенная ассоциативная система K будет иметь единицу (элемент, представленный пустым словом); элементы K
будет иметь единицу (элемент, представленный пустым словом); элементы K , представленные буквами алфавита А, будут составлять для K
, представленные буквами алфавита А, будут составлять для K систему порождающих элементов, а список соотношений о будет представлять собой полную систему соотношений между упомянутыми порождающими элементами K
систему порождающих элементов, а список соотношений о будет представлять собой полную систему соотношений между упомянутыми порождающими элементами K в том смысле, что элементы K
в том смысле, что элементы K , представленные словами Р и Q, тождественны в K
, представленные словами Р и Q, тождественны в K тогда и только тогда, когда Р и Q эквивалентны в
тогда и только тогда, когда Р и Q эквивалентны в  . Таким образом, распознавание тождества элементов в K
. Таким образом, распознавание тождества элементов в K сводится к распознаванию эквивалентности слов в
сводится к распознаванию эквивалентности слов в  . Отсюда становится понятной важность исследования разрешимости алгоритмической проблемы распознавания эквивалентности слов в произвольном А. и. Эта проблема была впервые сформулирована А. Туэ [1]; она заключается в том, что для Произвольного А. и.
. Отсюда становится понятной важность исследования разрешимости алгоритмической проблемы распознавания эквивалентности слов в произвольном А. и. Эта проблема была впервые сформулирована А. Туэ [1]; она заключается в том, что для Произвольного А. и.  требуется построить алгоритм, к-рый для любой пары слов в алфавите А. и.
требуется построить алгоритм, к-рый для любой пары слов в алфавите А. и.  позволял бы за конечное число шагов выяснить, эквивалентны ли в
позволял бы за конечное число шагов выяснить, эквивалентны ли в  слова, составляющие эту пару. В алгебраич. интерпретации эта проблема есть проблема тождества для ассоциативной системы K
слова, составляющие эту пару. В алгебраич. интерпретации эта проблема есть проблема тождества для ассоциативной системы K . Самому А. Туэ удалось решить ее лишь в весьма частных случаях. В современной интерпретации (после 30-х гг. 20 в.) этой проблемы алгоритм ищется в к.-л. точном смысле слова, напр. частично рекурсивная функция, Тьюринга машина или нормальный алгорифм. При такой модернизации этой проблемы уже становится осмысленным вопрос о том, нельзя ли указать такое конкретное А. и., для к-рого искомый алгоритм оказался бы невозможным. А. А. Марковым [3] и Э. Постом [4] одновременно и независимо были построены неразрешимые А. и., то есть А. и. с неразрешимой алгоритмия. проблемой распознавания эквивалентности слов. Эти результаты дают отрицательное решение модернизированной проблемы А. Туэ. Однако, принимая Чёрча тезис или к.-л. другое, эквивалентное ему предложение считать произведенное в теории алгоритмов уточнение понятия алгоритма адекватным, мы с необходимостью приходим к заключению, что и в начальной постановке проблема Туэ для нек-рого конкретного А. и. решается отрицательно.
. Самому А. Туэ удалось решить ее лишь в весьма частных случаях. В современной интерпретации (после 30-х гг. 20 в.) этой проблемы алгоритм ищется в к.-л. точном смысле слова, напр. частично рекурсивная функция, Тьюринга машина или нормальный алгорифм. При такой модернизации этой проблемы уже становится осмысленным вопрос о том, нельзя ли указать такое конкретное А. и., для к-рого искомый алгоритм оказался бы невозможным. А. А. Марковым [3] и Э. Постом [4] одновременно и независимо были построены неразрешимые А. и., то есть А. и. с неразрешимой алгоритмия. проблемой распознавания эквивалентности слов. Эти результаты дают отрицательное решение модернизированной проблемы А. Туэ. Однако, принимая Чёрча тезис или к.-л. другое, эквивалентное ему предложение считать произведенное в теории алгоритмов уточнение понятия алгоритма адекватным, мы с необходимостью приходим к заключению, что и в начальной постановке проблема Туэ для нек-рого конкретного А. и. решается отрицательно.
Первоначальные примеры А. А. Маркова и Э. Поста были чрезвычайно сложными. В дальнейшем предложены более простые неразрешимые А. и. ; напр., А. и. с семью весьма простыми соотношениями (см. [5]), с всего лишь тремя соотношениями (см. [6]); почти полностью решена проблема Туэ в случае А. и. с одним соотношением (см. [7]).
Естественным образом определяется изоморфизм одного А. и. в другое А. и., а также на другое А. и. (см., напр., 12], с. 331-34). С алгебраич. точки зрения особый интерес представляет рассмотрение таких свойств А. и., к-рые являются инвариантными относительно изоморфизмов: эти свойства суть свойства абстрактных ассоциативных систем. А. А. Марков (см. [2], с. 331-70), основываясь на своих исследованиях по проблеме распознавания эквивалентности слов в А. и., получил весьма общий результат, дающий отрицательное решение практически всех обсуждавшихся в то время алгоритмич. проблем, связанных с основными классификациями А. и. В частности, он показал, что если И - инвариантное свойство А. и. и имеется единичное А. и. со свойством И, а также - А. и., не включаемое ни в какое А. и. со свойством И, то для всякого алфавита с числом букв более трех алгоритмич. проблема распознавания А. и. со свойством И среди прочих А. и. неразрешима. Из этого результата непосредственно вытекает неразрешимость (для всякого алфавита, содержащего более трех букв) алгоритмич. проблем распознавания единичности А. и., конечности А. и., полугрупповости А. и., включаемости в групповое А. и., изоморфии для пар А. и. Впоследствии было показано (см. [8]), что множество пар изоморфных А. и. является рекурсивно перечислимым; использованный при этом метод позволяет также установить рекурсивную перечислимость ряда инвариантных свойств А. и.
Лит. : [1] Thue А., «Videnskapsselskapets Skrifter. 1. Mat Naturv. Kl. », 1914, № 10; [2] Mapков А., А., Теория алгорифмов, M., 1954 («Тр. Матем. ин-та АН СССР», т. 42); [3] его же, «Докл. АН СССР», 1947, т. 55, № 7, с. 587-90; [4] Post Е. L., «J. Symb. Logic», 1947, v. 12, p. 1-11; [5] Цейтин Г. С. «Докл. АН СССР», 1956, т. 107, № 3, с. 370-71; [6] Матиясевич Ю. В., «Докл. АН СССР», 1967, т. 173, № 6, с. 1264-66; [7] Адян С. И., «Тр. Матем. ин-та АН СССР», 1966, т. 85 с. 1-123; [8] Нагорный Н. М., «Z. math. Logik und Grundl. Math. », 1960, Bd 6, S. 319-24.
H. M. Нагорный.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'