АСИМПТОТИЧЕСКОЕ РАВЕНСТВО

Расстановка ударений: АСИМПТОТИ`ЧЕСКОЕ РА`ВЕНСТВО

АСИМПТОТИЧЕСКОЕ РАВЕНСТВО функций f(x) и g (х) при х → х₀ означает, что в нек-рой окрестности точки х₀ (за исключением, быть может, самой точки х₀)

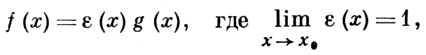
т. е. что

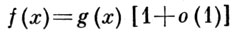
при х → х₀ (х₀ - конечная или бесконечная предельная точка множества, на к-ром определены рассматриваемые функции). Если функция g(x) не обращается в нуль в нек-рой окрестности точки х₀, то это условие равносильно требованию

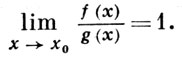
Иначе говоря, А. р. функций f(x) и g(x) при х → x₀ означает в этом случае, что относительная погрешность приближенного равенства функций f(x) и g(x), т. е. величина [f(x) - g(x)]/g(х), g(x) ≠ 0, является бесконечно малой при х → х₀ . А. р. функций содержательно для бесконечно малых и бесконечно больших функций. А. р. функций f(x) и g(x) обозначается f(x)~g(x) при х → х₀ и обладает свойствами рефлексивности, симметричности и транзитивности. В силу этого совокупность бесконечно малых (бесконечно больших) при х → х₀ функций распадается на классы эквивалентности бесконечно малых (бесконечно больших). Примером асимптотически равных функций (они наз. также эквивалентными) при х → х₀ являются функции u(х), sin u(x), ln [1 + u(х)], е^u(x) - 1, где lim u(х) = 0.

Если f~f₁ и g~g₁ при х → х₀, то

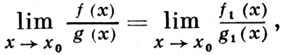
причем из существования каждого из написанных пределов следует существование другого. См. также Асимптотическое разложение функций, Асимптотическая формула.

М. И. Шабунин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.