АСИМПТОТИЧЕСКОЕ ЗНАЧЕНИЕ

Расстановка ударений: АСИМПТОТИ`ЧЕСКОЕ ЗНАЧЕ`НИЕ

АСИМПТОТИЧЕСКОЕ ЗНАЧЕНИЕ - предельное значение вдоль нек-рого пути. Точнее, комплексное число α или α = ∞ наз. А. з. функции f(z) комплексного переменного z в точке а замыкания D области определения D, если существует путь L : z = z(t), 0 ≤ t < 1, L ⊂ D, оканчивающийся в точке а,

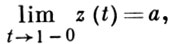
вдоль к-рого

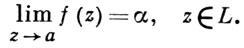
Напр., функция f(z) = e^z в точке а = ∞ имеет А. з. α₁ = 0 и α₂ = ∞ соответственно вдоль путей L₁ : z = - t, 0 ≤ t < + ∞, и L₂ : z = t, 0 ≤ t < + ∞. Множества А. з. играют важную роль в теории предельных множеств.

Если f(z) имеет в а два различных А. з., то а наз. точкой неопределенности функции f (z). Для произвольной функции f(z), определенной в плоской односвязной области, множество ее точек неопределенности не более чем счетно.

Данное выше определение А. з. относится к точечным А. з. Если кривая L имеет в качестве предельного множества не одну точку a ∈ ∂D, а нек-рое множество E ⊂ ∂D, то говорят также об А. з. А(f, Е), связанном с Е.

Лит. : [1] Коллингвуд Э., Ловатер А., Теория предельных множеств, пер. с англ., М., 1971; [2] Мак-Лейн Г., Асимптотические значения голоморфных функций, пер. с англ., М., 1966.

В. И. Гаврилов, Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.