АСИМПТОТИЧЕСКИ УСТОЙЧИВОЕ РЕШЕНИЕ

Расстановка ударений: АСИМПТОТИ`ЧЕСКИ УСТО`ЙЧИВОЕ РЕШЕ`НИЕ

АСИМПТОТИЧЕСКИ УСТОЙЧИВОЕ РЕШЕНИЕ - решение дифференциальной системы, устойчивое по Ляпунову (см. Устойчивость по Ляпунову) и притягивающее все остальные решения с достаточно близкими начальными значениями. Таким образом, решение

x (τ, ξ₀), x (α, ξ₀) = ξ₀,

системы

(*)

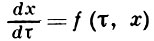
с правой частью f(τ, ξ), заданной для всех τ ≥ α, ξ ∈ ℝⁿ и обеспечивающей существование и единственность решений системы (*), будет А. у. р., если оно вместе со всеми достаточно близкими решениями

x (τ, ξ), |ξ - ξ₀| < h, h > 0,

определено для всех τ ≥ α и если для любого ε > 0 существует δ, 0 < δ < h такое, что |ξ - ξ₀ | < δ влечет

||x (τ, ξ) - x (τ, ξ₀)|| < ε

для всех τ ≥ α и

x (τ, ξ) - x (τ, ξ₀)|| → 0 при τ → +∞.

Понятие А. у. р. введено А. М. Ляпуновым [1]; оно широко используется в теории устойчивости наряду с различными специальными типами равномерной асимптотич. устойчивости (см. [2]).

Лит. : [1] Ляпунов А. М., Собр. соч., т. 2, М. - Л., 1956; [2] Красовский Н. Н., Некоторые задачи теории устойчивости движения, М., 1959.

Ю. С. Богданов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.