АСИМПТОТИЧЕСКАЯ ПРЕНЕБРЕГАЕМОСТЬ

Расстановка ударений: АСИМПТОТИ`ЧЕСКАЯ ПРЕНЕБРЕГА`ЕМОСТЬ

АСИМПТОТИЧЕСКАЯ ПРЕНЕБРЕГАЕМОСТЬ - свойство случайных величин, указывающее на их индивидуально малый вклад в качестве отдельных компонент в их сумму. Это понятие существенно, напр., в так наз. схемах серий. Именно, пусть случайные величины X_nk (n = 1, 2,...; k = 1, 2, ..., k_n) взаимно независимы при каждом n, и

S_n = X_n1 + ... + X_nkn.

Если для любых ε > 0 и δ > 0 при достаточно больших n выполняется неравенство

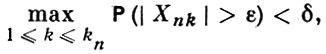
(1)

то отдельные слагаемые S_n наз. А. п. (величины Х_nk образуют при этом так наз. нулевую схему серий). При условии (1) справедлив следующий важный результат: класс предельных распределений для S_n - А_n (А_n - нек-рые «центрирующие» константы) совпадает с классом безгранично делимых распределений. Если распределения S_n сходятся к предельному, k_n → ∞ и слагаемые одинаково распределены, то условие (1) автоматически выполняется. Если усилить требование А. п., предполагая, что для любых ε > 0 и δ > 0 при всех достаточно больших n

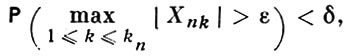
(2)

то будет верно утверждение: при условии (2) предельным распределением для S_n - A_n может быть только нормальное распределение (в частности, с дисперсией, равной нулю, т. е. вырожденное распределение).

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.