АСИМПТОТИЧЕСКАЯ ПЛОТНОСТЬ

Расстановка ударений: АСИМПТОТИ`ЧЕСКАЯ ПЛО`ТНОСТЬ

АСИМПТОТИЧЕСКАЯ ПЛОТНОСТЬ - разновидность общего понятия плотности последовательности натуральных чисел, к-рое является мерой того, какая часть последовательности всех натуральных чисел принадлежит заданной последовательности А натуральных чисел со включением нуля. Асимптотическая плотность последовательности А выражается действительным числом α, определяемым формулой

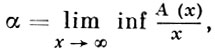
где

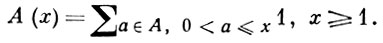
Число

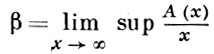
наз. верхней А. п. Если числа α и β совпадают, то их общее значение наз. натуральной плотностью. Напр., последовательность чисел, свободных от квадратов, имеет натуральную плотность δ = 6/π² . Понятие А. п. используется при нахождении критериев того, чтобы нек-рая последовательность была асимптотическим базисом.

Б. М. Бредихин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.