АСИММЕТРИИ КОЭФФИЦИЕНТ

Расстановка ударений: АСИММЕ`ТРИИ КОЭФФИЦИЕ`НТ

АСИММЕТРИИ КОЭФФИЦИЕНТ - наиболее употребительная мера асимметрии распределения, определяемая отношением

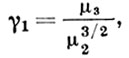
где μ₂ и μ₃ - второй и третий центральные моменты распределения, соответственно.

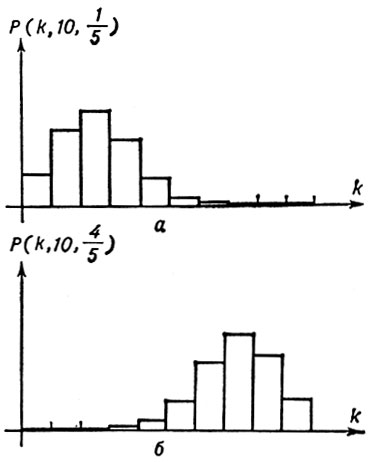
Графики биномиального распределения Р (k, n, р), соответствующего n = 10 испытаниям Бернулли, с (а) положительной асимметрией (p = 1/5) и (б) отрицательной асимметрией (p = 4/5).

Для распределений, симметричных относительно математич. ожидания, γ₁ = 0; в зависимости от знака γ₁ говорят о распределениях с положительной асимметрией (γ₁ > 0) и с отрицательной асимметрией (γ₁ < 0). Для биномиального распределения, соответствующего n Бернулли испытаниям с вероятностью успеха р,

(*)

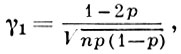
при этом в случае р = 1/2 (γ₁ = 0) распределение симметрично, в случаях р < 1/2 и р > 1/2 получаются типичные графики распределения с положительной (рис. а) и отрицательной (рис. б) асимметрией. А. к. γ₁ стремится к нулю при n → ∞ в соответствии с тем, что нормированное биномиальное распределение сходится к стандартному нормальному.

А. к. вместе с эксцесса коэффициентом - наиболее употребительные характеристики точности, с к-рой функция распределения F_n (х) суммы

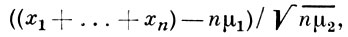
где (x₁, ..., x_n) - выборка из распределения, имеющего конечные моменты μ₁, ..., μ_r, r > 2, может быть приближена функцией нормального распределения

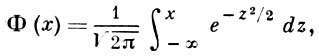
а именно, при довольно общих условиях Эджворта ряд дает

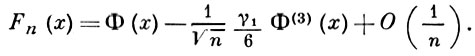
Лит. : [1] Крамер Г., Математические методы статистики, пер. с англ., М., 1948, с. 253-56; [2] Уилкс С., Математическая статистика, пер. с англ., М., 1967, с. 273-77.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.