АРХИМЕДОВА СПИРАЛЬ

Расстановка ударений: АРХИМЕ`ДОВА СПИРА`ЛЬ

АРХИМЕДОВА СПИРАЛЬ - плоская трансцендентная кривая, уравнение к-рой в полярных координатах имеет вид:

ρ = аφ.

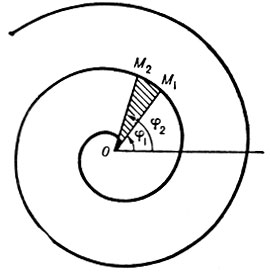
А. с. описывается точкой М, движущейся равномерно по прямой d, к-рая вращается вокруг точки О, принадлежащей этой прямой. В начальный момент движения М совпадает с центром вращения О прямой (см. рис.). Длина дуги между точками М₁ (ρ₁, φ₁) и М₂ (ρ₂, φ₂):

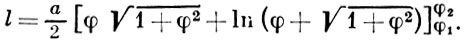
Площадь сектора, ограничиваемого дугой А. с. и двумя радиус-векторами ρ₁ и ρ₂, соответствующими углам φ₁ и φ₂ :

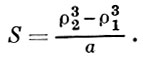
А. с. относится к так наз. алгебраич. спиралям (см. Спирали). Обобщение А. с - неоида, уравнение к-рой в полярных координатах

ρ = аφ + l.

А. с. названа по имени Архимеда (3 в. до н. э.), изучавшего ее свойства.

Лит. : [1] Савелов А. А., Плоские кривые. Систематика, свойства, применения, М., 1960.

Д. Д. Соколов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.