АРХИМЕДОВА ПОЛУГРУППА

Расстановка ударений: АРХИМЕ`ДОВА ПОЛУГРУ`ППА

АРХИМЕДОВА ПОЛУГРУППА - 1) Линейно упорядоченная полугруппа, все строго положительные (строго отрицательные) элементы к-рой принадлежат одному архимедову классу. Всякая естественно упорядоченная А. п. S (см. Естественно упорядоченный группоид) изоморфна нек-рой подполугруппе одной из следующих полугрупп: аддитивной полугруппе всех неотрицательных действительных чисел, полугруппе всех действительных чисел интервала (0, 1) с обычной упорядоченностью и операцией ab = min (a + b, 1), полугруппе состоящей из всех действительных чисел интервала (0, 1) и символа ∞ с обычной упорядоченностью и операцией

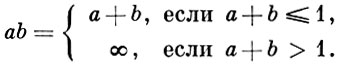
Первый случай имеет место тогда и только тогда, когда S - полугруппа с сокращением.

Лит. : [1] Фукс Л., Частично упорядоченные алгебраические системы, пер. с англ., М., 1965.

О. А. Иванова.

2) Полугруппа S, удовлетворяющая условию: для любых a, b ∈ S существует такое натуральное число n, что aⁿ ∈ SbS. При условии аⁿ ∈ Sb(aⁿ ∈ bS) полугруппа S наз. архимедовой слева (справа). Для коммутативных полугрупп все эти понятия эквивалентны. Любая коммутативная полугруппа S единственным образом разложима в связку А. п. (причем такое разложение совпадает с наиболее дробным разложением S в связку полугрупп). Этот результат по-разному обобщался на некоммутативные полугруппы (см. [1]). Полугруппа S с идемпотентом будет архимедовой (архимедовой справа) тогда и только тогда, когда она обладает ядром К, причем К содержит идемпотент (K есть правая группа), а факторполугруппа Риса (см. Полугруппа) S/К есть нильполугруппа. А. п. без идемпотентов труднее поддаются изучению. Лишь в коммутативном случае здесь дано полное описание в терминах нек-рых конструкций, особенно прозрачное для полугрупп с законом сокращения (см. [2], § 4. 3; [3]).

Лит. : [1] Putcha M. S., «Semigroup Forum», 1973, v. 6, № 3, p. 232-39; [2] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [3] Tarnurа Т., «Math. Nachr. », 1968, Bd 36, № 5/6, S. 255-87.

Л. H. Шеврин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.