АРХИМЕДОВ КЛАСС

Расстановка ударений: АРХИМЕ`ДОВ КЛА`СС

АРХИМЕДОВ КЛАСС - класс разбиения, индуцируемого архимедовым отношением эквивалентности на линейно упорядоченной полугруппе. Эта эквивалентность определяется следующим образом: элементы a, b полугруппы S наз. архимедово эквивалентными, если имеет место одно из следующих четырех соотношений:

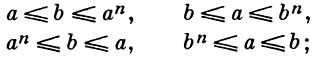
это равносильно тому, что а и b порождают одну и ту же выпуклую подполугруппу в S. Таким образом, разбиение на А. к. является разбиением на попарно непересекающиеся выпуклые подполугруппы, причем каждое разбиение S на попарно непересекающиеся выпуклые подполугруппы может быть продолжено до разбиения на А. к.

Архимедова эквивалентность на линейно упорядоченной группе индуцируется архимедовой эквивалентностью ее положительного конуса: считается, что a~b, если существуют такие положительные целые числа m и n, что

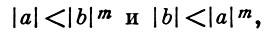
где

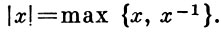
Положительный конус архимедовой группы состоит из одного А. к.

О. А. Иванова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.