АРКСИНУСА ЗАКОН

Расстановка ударений: АРКСИ`НУСА ЗАКО`Н

АРКСИНУСА ЗАКОН - предельная теорема, описывающая флуктуации случайного блуждания на прямой, приводящая к арксинуса распределению или обобщенному распределению арксинуса. В 1939 П. Леви (P. Levy) для процесса броуновского движения {ξ_t, t ≥ 0, ξ₀ = 0} отметил следующий факт. Пусть τ_t - мера Лебега множества {u : ξ_u > 0, 0 ≤ u ≤ t}, другими словами, время, проведенное броуновской частицей на положительной полуоси за промежуток времени [0, t]. Тогда отношение τ_t /t имеет распределение арксинуса:

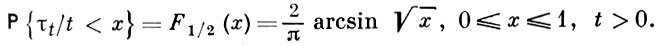
Позднее было обнаружено (см. [2]), что для случайного блуждания с дискретным временем имеет место следующий закон арксинуса: пусть S₀ = 0, S₁, ..., S_n,... - последовательные положения в случайном блуждании,

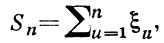
ξ₁, ..., ξ_n,... независимы и одинаково распределены, Т_n равно числу индексов к среди 0, 1, ..., n, для к-рых S_k > 0,

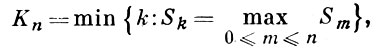
тогда соотношения

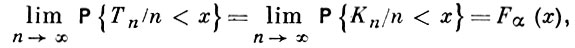
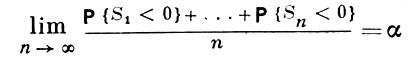
выполняются или не выполняются одновременно, где F_α (x) при 0 < α < 1 - обобщенное распределение арксинуса,

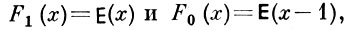
при этом Е(х) = 0 при x ≤ 0 и E(х) = 1 при х > 0.

А. з. в теории восстановления утверждает, что при 0 < α < 1 имеют место равенства:

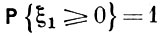
и

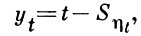
где η_t определяется соотношением S_ηt < t ≤_{ηt + 1},

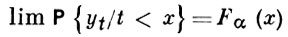
тогда и только тогда, когда

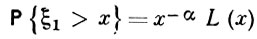
при х > 0, где L(х) - функция, определенная при х > 0 и обладающая свойством

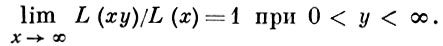
Существует тесная связь между А. з. в теории восстановления и для случайных блужданий (см. [3]).

Лит. : [1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 2, М., 1967; [2] Спицер Ф., Принципы случайного блуждания, пер. с англ., М., 1969; [3] Рогозин Б. А., «Теория вероятн. и ее примен. », 1971, т. 16, № 4, С. 593-613.

Б. А. Рогозин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.