АРИФМЕТИКА ФОРМАЛЬНАЯ

Расстановка ударений: АРИФМЕ`ТИКА ФОРМА`ЛЬНАЯ

АРИФМЕТИКА ФОРМАЛЬНАЯ, арифметическое исчисление, - логико-математич. исчисление, формализующее элементарную теорию чисел. Язык наиболее употребительного варианта А. ф. содержит константу 0, числовые переменные, символ равенства, функциональные символы +, ⋅, ' (прибавление 1) и логич. связки. Термы строятся из константы 0 и переменных с помощью функциональных символов; в частности, натуральные числа изображаются термами вида 0'^... '. Атомарные формулы - это равенства термов; остальные формулы строятся из атомарных с помощью логич. связок &, ∨, →, ⌉, ∀, ∃. Формулы в языке А. ф. наз. арифметическими формулами. Постулатами А. ф. являются постулаты предикатов исчисления (классического или интуиционистского в зависимости от того, какая А. ф. рассматривается), аксиомы Пеано

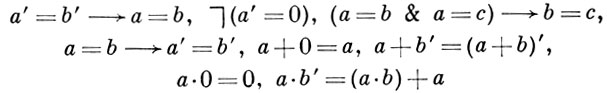
и схема аксиом индукции

где А - произвольная формула, наз. индукционной формулой.

Средства А. ф. оказываются достаточными для вывода теорем, устанавливаемых в стандартных курсах элементарной теории чисел. В настоящее время (1970-е гг.), по-видимому, неизвестно ни одной содержательной теоретико-числовой теоремы, доказанной без привлечения средств анализа, к-рая не была бы выводима в А. ф. Запись и доказательство таких теорем в А. ф. требует выявления ее выразительных возможностей. Особенно существенна выразимость в А. ф. многих теоретико-числовых функций. В частности, в А. ф. можно записывать суждения о примитивно (и даже частично) рекурсивных функциях. При этом оказываются выводимыми формулы, выражающие важные свойства частично рекурсивных функций, в частности их определяющие равенства. Так, равенство f(x') = g(x, f(x)) выражается формулой

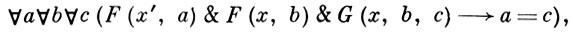
где F и G - формулы, изображающие графики функций f и g, соответственно. В А. ф. можно формулировать суждения о конечных множествах. Более того, классич. А. ф. эквивалентна аксиоматической теории множеств Цермело-Френкеля без аксиомы бесконечности: в каждой из этих систем может быть построена модель другой.

Дедуктивная сила системы А. ф. характеризуется ординалом ε₀ (наименьшее решение уравнения ω^ε = ε): в А. ф. выводима схема трансфинитной индукции до любого ординала α < ε₀, но не выводима схема индукции до ε₀ . Класс доказуемо рекурсивных функций системы А. ф. (т. е. частично рекурсивных функций, общерекурсивность к-рых может быть установлена средствами А. ф.) совпадает с классом ординально рекурсивных функций с ординалами < ε₀ . Это позволяет погружать в А. ф. нек-рые ее расширения, напр. А. ф. с символами для всех примитивно рекурсивных функций и соответствующими дополнительными постулатами. А. ф. удовлетворяет условиям обеих Гёделя теорем о неполноте. В частности, имеются такие полиномы Р, Q от нескольких переменных, что формула ∀ X(Р (Х) ≠ Q(X)) невыводима, хотя и выражает истинное утверждение, а именно непротиворечивость системы А. ф.

При исследовании структуры А. ф. (в частности, вопросов непротиворечивости) используется ее формулировка без кванторов, но с гильбертовским ε-символом. При построении формул этой системы не допускается употребление кванторов, но разрешается использование термов вида ε_x А (х) (нек-рое х, удовлетворяющее условию А, если такие х существуют, и 0 в противном случае). Постулаты ε-системы - это постулаты исчисления высказываний, правила для равенства, правило подстановки вместо свободной числовой переменной, аксиомы для функций +, ⋅, ', pd (вычитание 1 из положительных чисел) и следующие ε-аксиомы:

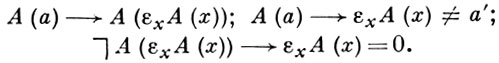
Кванторы вводятся как сокращения:

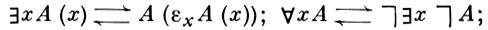
аксиома индукции оказывается выводимой.

Формулы А. ф., содержащие свободные переменные, задают теоретико-числовые предикаты. Формулы, не содержащие свободных переменных (замкнутые формулы), выражают суждения, k-местный предикат 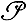от натуральных чисел наз. арифметическим, если найдется такая арифметич. формула Р(x₁, ..., x_k), что для любых натуральных чисел n₁, ..., n_k имеет место

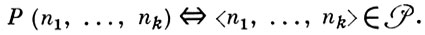
Это определяет классификацию арифметич. предикатов по типу префикса в предваренной форме соответствующей формулы. Класс ∑_n (класс П_n) состоит из предикатов Р(α), изобразимых формулой вида

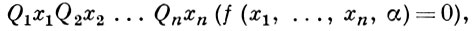
где f - примитивно рекурсивная функция, Q₁ есть ∃ (соответственно ∀) и Q_i - чередующиеся кванторы (т. е. Q_{i + 1} есть Q^→_i, где ∀¯ есть ∃, а ∃¯ есть ∀). Каждый из этих классов содержит универсальный предикат, т. е. такой предикат Т(е, а), что для всякого одноместного предиката Р из того же класса имеется число е_P, для к-рого верно ∀ х((Т(е_P, х) ≡ Р(х)). Многоместные предикаты сводятся к одноместным с помощью функций, нумерующих системы натуральных чисел. При каждом n > 0 справедливо неравенство ∑_n ≠ П_n, и класс с меньшим индексом есть собственная часть любого класса с большим индексом. Классификация предикатов порождает классификацию арифметич. функций на основе классификации соответствующих графиков. Не все теоретико-числовые предикаты арифметические: примером неарифметич. предиката является такой предикат Т(х), что для любой замкнутой арифметич. формулы А имеет место Т (⌜ А⌝) = А, где ⌜ А⌝ - номер формулы А в нек-рой фиксированной нумерации, удовлетворяющей естественным условиям. Предикат Т играет существенную роль в исследованиях структуры А. ф., в частности вопроса о независимости ее аксиом. Присоединение к А. ф. символа T с аксиомами типа T(⌜ A&B⌝) = T(⌜ А⌝)&T(⌜ B⌝), выражающими его перестановочность с логич. связками, позволяет доказать непротиворечивость А. ф. Та же конструкция (но уже внутри А. ф.) проходит для подсистемы A_[n] системы А. ф., в к-рой схема индукции ограничена условием: индукционная формула имеет сложность ≤ n, т. е. принадлежит ∑_n ∪ П_n . Роль T здесь успешно исполняет, напр., универсальный предикат для ∑_{n + 1} и соответствующее доказательство проводится в системе A_{[n + 1]} . В силу второй теоремы Гёделя о неполноте отсюда следует, что A_{[n + 1]} сильнее A_[n], так что А. ф. не совпадает ни с одной из систем A_[n] и схему индукции нельзя заменить никаким конечным множеством аксиом. А. ф. оказывается полной относительно формул из класса ∑₁ : замкнутая формула из этого класса выводима в А. ф. тогда и только тогда, когда она истинна. Так как класс ∑₁ содержит алгорифмически неразрешимый предикат, отсюда следует, что проблема выводимости в А. ф. алгорифмически неразрешима.

При задании А. ф. в виде Генцена формальной системы обычного типа сечение оказывается неустранимым. Устранение сечения становится возможным, если заменить схему индукции правилом бесконечной индукции (ω-правило):

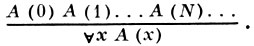
На этом пути было получено одно из первых доказательств непротиворечивости А. ф. При фактическом построении системы с ω-правилом основным оказывается предикат «число е есть номер общерекурсивной функции, описывающей вывод длины < ε₀ с ω-правилом (ω-вывод)». Этот предикат принадлежит классу П₂, и получающаяся система оказывается не формальной, а лишь полуформальной. Каждому выводу формулы A в А. ф. удается сопоставить такое число е, что суждение «e есть ω-вывод формулы A без сечения» истинно (и даже доказуемо в А. ф.). Так как ω-вывод без сечения замкнутой бескванторной формулы не содержит кванторов, отсюда следует непротиворечивость А. ф. Применение второй теоремы Гёделя о неполноте позволяет получить отсюда, что теорема об устранении сечения из любого вывода в А. ф. не может быть доказана средствами А. ф. ; тем не менее это может быть доказано в А. ф. при любом фиксированном N для любого вывода с индукциями сложности ≤ N. Переход к ω-выводам позволяет устанавливать многие метаматематич. теоремы о системе А. ф., в частности полноту относительно формул из ∑₁ и ординальную характеристику доказуемо рекурсивных функций.

Лит. : [1] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [2] Нilbеrt D., Bernays P., Grundlagen der Mathematik, 2 Aufl., Bd 1-2, В., 1968-70; [3] Hовиков П. С., Элементы математической логики, 2 изд., М., 1973; [4] Kreisel G., «J. Symbolic Logic», 1968, v. 33, № 3, p. 321 - 88; [5] Гёдель К., в сб. : Математическая теория логического вывода, М., 1967, с. 299 - 310.

Г. Е. Минц.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.