АРБИТРАЖНАЯ СХЕМА

Расстановка ударений: АРБИТРА`ЖНАЯ СХЕ`МА

АРБИТРАЖНАЯ СХЕМА - правило, по к-рому каждой игре с дележами (см. Кооперативная игра) ставится в соответствие единственный дележ этой игры, наз. арбитражным решением. Первоначально А. с. были рассмотрены Дж. Нэшем [1] для случая игры двух лиц. Пусть u = {u(u₁, ..., u_n)} - множество дележей, d = (d₁, ..., d_n) - точка status quo, т. е. точка, соответствующая случаю, когда никакой дележ не осуществляется, [R, d] - игра с дележами, u - ее арбитражное решение. Дележ u* наз. решением Нэша, если

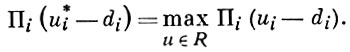
Решение Нэша и только оно удовлетворяет следующим аксиомам: 1) если f - линейное неубывающее преобразование, то fu¯ есть арбитражное решение игры [fR, fd] (инвариантность относительно преобразований полезности); 2) u¯ ≥ d, u¯ ∈ R и нет такого u ∈ R, чтобы u ≥ u¯ (оптимальность по Парето); 3) если R' ⊂ R, d' = d, u¯ ∈ R', то u¯ ' = u¯ (независимость несвязанных альтернатив); 4) если d_i = d_j, i, j = 1, ..., n и R симметрична, то u¯_i = u¯_j, i, j = 1, ..., n (симметрия).

Другую А. с. с характеристич. функцией v(S), S ⊂ N = (1, ..., n) для игр n лиц дал Л. С. Шепли [2]. Решение Шепли φ (v) = (φ₁ (v), ..., φ_n (v)), где

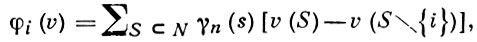
γ_n (s) = (s - 1)!(n - s)!/n!, s - число элементов множества S, также удовлетворяет аксиоме симметрии, кроме того, ∑_i φ_i (v) = v(N) и для любых двух игр u и v выполняется φ (u + v) = φ (u) + φ (v). Были также рассмотрены А. с. для случая сравнимых индивидуальных выигрышей (см. [3]).

Арбитражные схемы Дж. Нэша и Л. С. Шепли обобщил Дж. Харшаньи [4]. Решение Харшаньи, кроме соответствующих четырех аксиом Нэша, удовлетворяет еще двум аксиомам: 1) решение монотонно зависит от обоснованных требований игрока, 2) если u* и u** - решения, то решением будет и u¯,

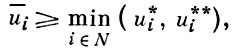
если только u¯ принадлежит границе множества R.

А. с. непрерывно зависят от параметров игры, если в R имеются лучшие дележи, чем точка status quo.

Лит. : [1] Nash J., «Econometrica», 1950, т. 18, № 2, p. 155-62; [2] Shapleу L. S., в кн. : Contributions to the theory of games, v. 2, Princeton (N. J.), 1953, p. 307-17; [3] Raiffa H., в кн. : Contributions to the theory of games, v. 2, Princeton (N. J.), 1953, p. 361-87; [4] Harsanyi J. C, в кн. : Contributions to the theory of games, v. 4, Princeton (N. J.), 1959, p. 325-55.

Э. Й. Вилкас.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.