АППРОКСИМАЦИЯ ПЕРИОДИЧЕСКИМИ ПРЕОБРАЗОВАНИЯМИ

Расстановка ударений: АППРОКСИМА`ЦИЯ ПЕРИОДИ`ЧЕСКИМИ ПРЕОБРАЗОВА`НИЯМИ

АППРОКСИМАЦИЯ ПЕРИОДИЧЕСКИМИ ПРЕОБРАЗОВАНИЯМИ - один из методов в эргодической теории. Любой автоморфизм Т пространства Лебега X с мерой μ может быть получен как предел периодич. автоморфизмов Т_n в естественной для пространства 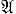всех автоморфизмов топологии, слабой или равномерной (см. [1]). При количественной характеристике скорости аппроксимации наряду с автоморфизмами Т_n рассматривают инвариантные относительно Т_n конечные измеримые разбиения X, т. е. разбиения μ пространства X на конечное число непересекающихся измеримых множеств C_{n, 1}, ..., C_{n, qn}, которые автоморфизм Т_n переводит друг в друга. Величина

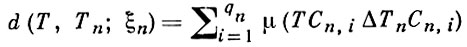
оценивает близость T_n к T относительно разбиения ξ_n ; здесь А - симметрическая разность:

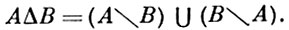
При фиксированном q_n можно подобрать такие ξ_n и Т_n (с указанными выше свойствами), что d(T, Т_n ; ξ_n) будет сколь угодно мало (см. [1]). Содержательные инварианты автоморфизма Т возникают при рассмотрении такой бесконечной последовательности Т_n и ξ_n, что для любого измеримого множества А имеется последовательность множеств А_n, целиком состоящая из нек-рых С_{n, i} и аппроксимирующая А в том смысле, что

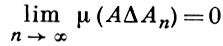
(«разбиения ξ_n сходятся к разбиению на точки»). Если при этом d(Т, Т_n ; ξ_n) < f(q_n), где f(n) - заданная монотонная последовательность, стремящаяся к нулю, то говорят, что T допускает А. п. п. I рода со скоростью f(n); если, сверх того, Т_n циклически переставляет множества С_{n, i}, то говорят о циклической А. п. п. Другие варианты см. в [2], [6], [7].

При определенной скорости аппроксимации те или иные свойства периодич. автоморфизмов Т_n влияют на свойства предельного автоморфизма Т. Напр., если Т допускает циклич. А. п. п. со скоростью с/n, то при с < 4 это гарантирует эргодичность Т, при с < 2 - отсутствие у Т перемешивания, а при с < 1 - простоту спектра соответствующего унитарного оператора сдвига. Нек-рые свойства Т могут быть охарактеризованы в терминах скорости аппроксимации. Напр., его энтропия равна нижней грани тех с, для к-рых Т допускает А. п. п. I рода со скоростью 2c/log₂ n (см. [2], [7]). А. п. п. применялась при исследовании ряда простых конкретных примеров (см. [2]), включая гладкие потоки на двумерных поверхностях (см., напр., [8]). При ее помощи был построен ряд динамич. систем с неожиданными метрич. свойствами (см. [2], [6], [7]) или с неожиданным сочетанием метрич. свойств с дифференциальными (см. [3], [4]).

Утверждение о плотности периодич. автоморфизмов в 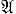, снабженном слабой топологией, может быть существенно усилено: для любой монотонной последовательности f(n) > 0 автоморфизмы, допускающие циклич. А. п. п. со скоростью f(n), образуют в 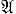множество II категории (см. [2]). Поэтому А. п. п. позволяет получать так наз. категорные теоремы, утверждающие, что в 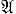(со слабой топологией) автоморфизмы с тем или иным свойством образуют множество I или II категории (напр., эргодическне множества - II категории, а перемешивающие - I категории, см. [1]).

Пусть X - топологическое или гладкое многообразие, а мера μ согласована с топологией или гладкостью. В классе гомеоморфизмов или диффеоморфизмов, сохраняющих μ, естественными являются не слабая, а другие топологии. Для гомеоморфизмов справедливы категорные теоремы, сходные с имеющимися для 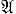(историю и современное состояние проблемы см. в [5]).

Лит. : [1] Халмош П., Лекции по эргодической теории, пер. с англ., М., 1959; [2] Каток А. Б., Стёпин А. М., «Успехи матем. наук», 1967. т. 22, № 5, с. 81-106; [3] Аносов Д. В., Каток А. Б., «Тр. Моск. матем. об-ва», 1970, т. 23, с. 3-36; [4] Каток А. Б., «Изв. АН СССР. Сер. матем. », 1973, т. 37, № 3, с. 539-76; [5] Каток А. Б., Стёпин А. М., «Успехи матем. наук», 1970, т. 25, 2, с. 193-220; [6] Аkсоglu М. A., Chacon R. V., Schwartzbauer Т., «Рrос. Amer. Math. Soc. », 1970, v. 24, № 3, p. 637-642; [7] Sсhwartzbаuer Т., «Pacific J. Math. », 1972, v. 43, № 3, p. 753-64; [8] Кочepгин А. В., «Матем. сб. », 1975, т. 96. № 3, с. 472-502.

Д. В. Аносов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.