
АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОЙ КРАЕВОЙ ЗАДАЧИ РАЗНОСТНОЙ
Расстановка ударений: АППРОКСИМА`ЦИЯ ДИФФЕРЕНЦИА`ЛЬНОЙ КРАЕВО`Й ЗАДА`ЧИ РА`ЗНОСТНОЙ
АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОЙ КРАЕВОЙ ЗАДАЧИ РАЗНОСТНОЙ - приближение дифференциального уравнения и краевых условий системой конечных (обычно алгебраических) уравнений относительно значений искомой функции на нек-рой сетке, к-рое уточняется при стремлении параметра разностной задачи (шага сетки) к нулю.
Пусть требуется вычислить функцию u, принадлежащую линейному нормированному пространству U функций, определенных в нек-рой области DU с границей Г, и являющуюся решением дифференциальной краевой задачи Lu = 0, lu|Г = 0, где Lu = 0 - дифференциальное уравнение, а lu|Г = 0 - совокупность граничных условий. Пусть DhU - сетка (см. Аппроксимация дифференциального оператора разностным) и Uh - линейное нормированное пространство функций uh, определенных на этой сетке. Норма в Uh вводится так, чтобы для любой функции v ∈ U выполнялось равенство
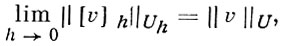
где [v]h - таблица значений функции v в точках сетки DhU - Задачу вычисления решения u заменяют нек-рой задачей ℒh uh = 0 приближенного вычисления таблицы [u]h значений решения u в точках сетки DhU . Здесь ℒh uh - нек-рая совокупность конечных (недифференциальных) уравнений относительно значений сеточной функции uh ∈ Uh .
Пусть vh - произвольная функция из Uh и ℒh vh = φh, Фh - линейное нормированное пространство, к-рому принадлежат при любом vh ∈ Uh . Говорят, что задача ℒh uh = 0 является разностной аппроксимацией порядка р дифференциальной краевой задачи Lu = 0, lu|Г = 0 на решении u последней, если
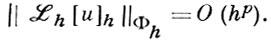
Фактическое построение системы ℒh uh = 0 разбивают на построение двух ее подсистем Lh uh = 0 и lh uh |Гh = 0. В качестве Lh uh = 0 используют к.-л. разностную аппроксимацию дифференциального уравнения (см. Аппроксимация дифференциального уравнения разностным). Дополнительные уравнения lh uh |Гh = 0 строят с использованием граничных условий lu|Г = 0.
А. д. к. з. р. в смысле приведенного определения ни при каком выборе норм в Uh и Фh еще не обеспечивают сходимости (см. [2]) решения uh разностной задачи к точному решению u, т. е. равенства
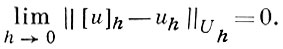
Дополнительным условием, обеспечивающим сходимость, является свойство устойчивости (см. [3], [5]-[8]), к-рым должна обладать разностная задача ℒh uh = 0. Задача ℒh uh = 0 наз. устойчивой, если существуют числа δ > 0 и h < h0 такие, что уравнение ℒh zh = φh имеет единственное решение zh ∈ Uh при любом φh ∈ Фh, ||φh || < δ, h < h0, причем это решение удовлетворяет неравенству
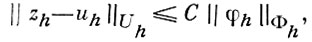
где С - нек-рая постоянная, не зависящая от h и возмущения правой части φh, a uh - решение невозмущенной задачи ℒh uh = 0. Если решение u дифференциальной задачи существует, а разностная задача ℒh uh = 0 аппроксимирует дифференциальную на решении u с порядком р и устойчива, то имеет место сходимость с тем же порядком, то есть
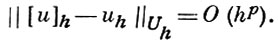
Напр., задача
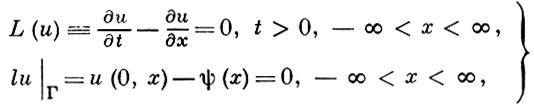
(1)
где ψ (х) - заданная функция, имеющая ограниченную производную 2-го порядка, при естественном определении норм аппроксимируется разностной задачей
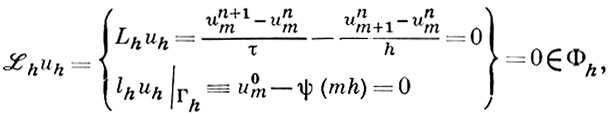
где unm - значение функции uh в точке (хm, tn) = (mh, nτ) сетки, τ = rh, r = const. Если за норму φn принять верхнюю грань модулей правых частей уравнений, составляющих систему ℒh vh = φh, vh ∈ Uh, то аппроксимация задачи (1) задачей (2) на решении u имеет первый порядок. При r > 1 сходимости нет ни при какой норме. При r ≤ 1 и норме
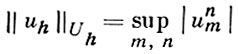
имеет место устойчивость и, следовательно, сходимость:
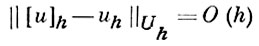
(см. [2], [3]).
Замена дифференциальных задач разностными является одним из наиболее универсальных средств приближенного вычисления решений дифференциальных краевых задач на ЭВМ (см. [7]).
Замену дифференциальных задач их разностными аналогами, начиная с работ [1], [2], [4], иногда удается использовать для самого доказательства существования решения дифференциальной задачи по следующей схеме. Устанавливается компактность зависящего от h семейства решений uh разностного аналога дифференциальной краевой задачи и доказывается, что пределом сходящейся при hk → 0 подпоследовательности uhk является решение u дифференциальной краевой задачи. Если известно, что оно единственно, то не только подпоследовательность, но и все семейство uh сходится к решению u при h → 0.
Лит: [1] Люстерник Л. А., «Успехи матем. наук», 1940, в. 8, с. 115-24; [2] Курант Р., Фридрихс К., Леви Г., «Успехи матем. наук», 1940, в. 8, с. 125-60; [3] Годунов С. К., Рябенький В. С., Разностные схемы. Введение в теорию, М., 1973; [4] Петровский И. Г., «Успехи матем. наук», 1940, в. 8, с. 161-70; [5] Рябенький В. С., «Докл. АН СССР», 1952, т. 86, № 6, с. 1071-3; [6] Рябенький В. С., Филиппов А. Ф., Об устойчивости разностных уравнений, М., 1956; [7] Самарский А. А., Введение в теорию разностных схем, М., 1971; [8] Филиппов А. Ф., «Докл. АН СССР», 1955, т. 100, № 6, с. 4045-8.
В. С. Рябенький.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'