АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РАЗНОСТНЫМ

Расстановка ударений: АППРОКСИМА`ЦИЯ ДИФФЕРЕНЦИА`ЛЬНОГО УРАВНЕ`НИЯ РА`ЗНОСТНЫМ

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ РАЗНОСТНЫМ - приближение дифференциального уравнения системой алгебраич. уравнений относительно значений искомых функции на нек-рой сетке, к-рое уточняется при стремлении параметра (шага сетки) к нулю.

Пусть L, Lu = f нек-рый дифференциальный оператор, a L_h, L_h u_h = f_h, u_h ∈ U_h, f_h ∈ F_h - нек-рый разностный оператор (см. Аппроксимация дифференциального оператора разностным). Говорят, что разностное уравнение L_h u_h = 0, 0 ∈ F_h аппроксимирует дифференциальное уравнение Lu = 0 на решении u с порядком h^p, если оператор L_h аппроксимирует оператор L на решении u с порядком р, т. е. если

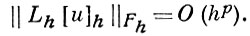
Простейший пример построения разностного уравнения L_h u_h = 0, аппроксимирующего дифференциальное уравнение Lu = 0 на решениях и, состоит в замене каждой производной, входящей в выражение Lu, аппроксимирующим ее разностным аналогом.

Напр., уравнение

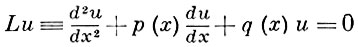
аппроксимируется со 2-м порядком разностным уравнением

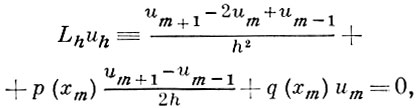
где сетки D_hU и D_hF состоят из точек x_m = mh, m - целое, u_m - значение функции u_h в точке x_m ; для уравнения

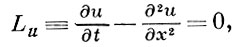
напр., двумя различными разностными аппроксимациями на гладких решениях являются:

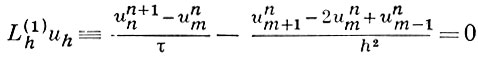
(явная схема), и

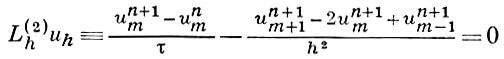
(неявная схема), где сетки D_hU и D_hF состоят из точек (х_m, t_n) = (mh, nτ), τ = rh², r = const, m и n - целые, а uⁿ_m- значение функции u_h в точке (х_m, t_n) сетки. Существуют разностные операторы L_h, аппроксимирующие дифференциальный оператор L особенно хорошо только на решениях u уравнения Lu = 0 и хуже на других функциях. Напр., оператор

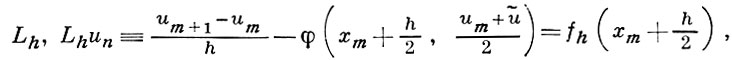
где ũ = u_m+ hφ (x_m) аппроксимирует оператор на

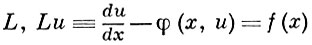
произвольных гладких функциях u(х) с первым порядком относительно h, а на решениях уравнения Lu = 0 со вторым [функция u(х) предполагается достаточно гладкой]. При численном решении краевых задач для дифференциального уравнения Lu = 0 с помощью разностного уравнения L_h u_h = 0 существенны свойства аппроксимации оператора L оператором L_h на решениях u уравнения Lu = 0, а не на произвольных гладких функциях. Для широкого класса дифференциальных уравнений и систем уравнений существуют способы построения аппроксимирующих их разностных уравнений, при к-рых выполняются различные дополнительные требования: устойчивость решения u_h относительно ошибок округления, допускаемых при вычислениях; выполнение для u_h тех или иных интегральных соотношений, имеющих место для решения u дифференциального уравнения; возможность использовать произвольные сетки D_hu и D_hF (важная при расчете движения сплошной среды); малое число арифметич. действий, необходимых для вычисления решения, и т. д.

А. д. у. р. является элементом аппроксимации дифференциальной краевой задачи разностной с целью приближенного вычисления решения первой.

Лит. : [1] Годунов С. К., Рябенький В. С., Введение в теорию разностных схем, М., 1962; [2] Самарский А. А., Введение в теорию разностных схем, М., 1971; [3] Годунов С. К. и др., Численное решение многомерных задач газовой динамики, М., 1976; [4] Самарский А. А., Попов Ю. П., Разностные схемы газовой динамики, М., 1975.

В. С. Рябенький.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.