АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА РАЗНОСТНЫМ

Расстановка ударений: АППРОКСИМА`ЦИЯ ДИФФЕРЕНЦИА`ЛЬНОГО ОПЕРА`ТОРА РА`ЗНОСТНЫМ

АППРОКСИМАЦИЯ ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА РАЗНОСТНЫМ - приближение дифференциального оператора таким зависящим от параметра оператором, результат применения к-рого к функции определяется ее значениями на нек-ром дискретном множестве точек - сетке, уточняющееся при стремлении параметра (шага сетки) к нулю.

Пусть L, Lu = f - дифференциальный оператор, переводящий каждую функцию и из класса функций U в функцию f из линейного нормированного пространства F. Пусть D_U - область определения функций из U и в D_U выделено нек-рое дискретное подмножество - сетка D_hU («сгущающаяся» при h → 0)). Рассматривается множество U_h всех функций [u]_h, определенных только на сетке и совпадающих в точках сетки с u. Разностным оператором наз. всякий оператор L_h, переводящий сеточные функции из U_h в функции f_h из F. Говорят, что оператор L_h, L_h [u]_h = f_h, аппроксимирует (аппроксимирует с порядком h^p) дифференциальный оператор L на классе U, если для любой функции u ∈ U при h → 0

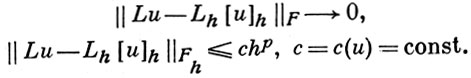
Иногда аппроксимацию понимают как равенство

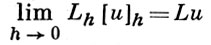
в смысле той или иной слабой сходимости. А. д. о. р. используется для приближенного вычисления функции Lu по таблице [u]_h значений функции и и для аппроксимации дифференциального уравнения разностным.

Существуют два основных приема построения оператора L_h, аппроксимирующего L.

Первый состоит в том, что определяют L_h [u]_h как результат применения дифференциального оператора L к функции из U, полученной с помощью той или иной интерполяционной формулы из сеточной функции [u]_h .

Второй способ состоит в следующем. В области D_F определения функции f из F вводят сетку D_hF и рассматривают линейное пространство F_h сеточных функций, определенных на D_hF . Оператор L_h [u]_h строят как произведение двух операторов: оператора, переводящего функцию [u]_h в сеточную функцию f_h из F_h, то есть в приближенную таблицу значений функции f(x), и оператора восполнения f_h с сетки D_hF на всю область D_F . Напр., для приближения оператора дифференцирования

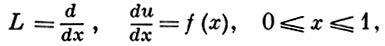
строится сетка D_hU, состоящая из точек x_k, k = 0, 1, ..., N,

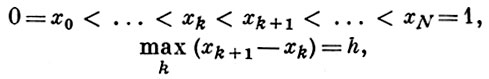
и сетка D_hF, состоящая из точек

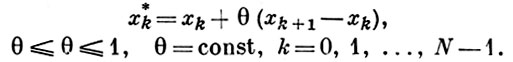
Значения оператора L_h [u]_h в точках х*_k определяются равенствами

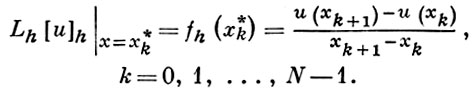
Затем L_h [u]_h доопределяется вне D_hF кусочно линейно с изломами, быть может, только в точках х*_k, k = 1, 2, ..., N - 2.

Пусть норма в F определяется формулой

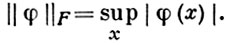
Тогда на классе функций U, имеющих ограниченную третью производную, при θ = 0 и θ = h/2 оператор L_h аппроксимирует 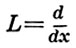с порядком h и h² соответственно. На классе U функций с ограниченными вторыми производными аппроксимация при любом θ ∈ [0, 1] имеет лишь первый порядок.

Иногда задачу А. д. о. р. условно считают решенной, если указан способ построения сеточной функции

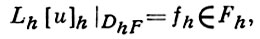
определенной только в точках сетки D_hF, оставляя задачу о восполнении функции f_h всюду на D_F вне рассмотрения. В таком случае для определения аппроксимации пространство F_h считают нормированным и притом относительно сетки и нормы предполагается, что для всякой функции f ∈ F совпадающая с ней в точках D_hF функция {f}_h ∈ F_h удовлетворяет равенству

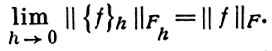
Оператор L_h понимают как оператор из U_h в F_h и говорят, что оператор L_h аппроксимирует (аппроксимирует с порядком h^p) дифференциальный оператор L на множестве U, если при h → 0

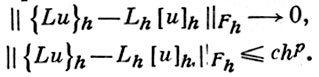
Для построения оператора L_h, аппроксимирующего L на достаточно гладких функциях с заданным порядком, часто прибегают к замене каждой производной, входящей в выражение L, ее разностной аппроксимацией, опираясь для этого на следующий факт. При любых натуральных i, j и при любом k₀, 2k₀ + 1 ≥ i + j в равенстве

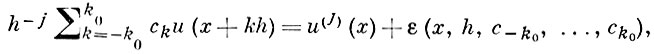
используя метод неопределенных коэффициентов и формулу Тейлора, можно так подобрать числа c_k, не зависящие от h, чтобы для любой функции u(х), имеющей j + r (r ≤ i) ограниченных производных, выполнялось неравенство вида

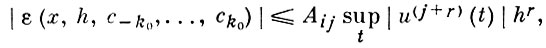
где A_ij зависит только от i и j. Напр., пусть требуется построить аппроксимирующий оператор для оператора Лапласа

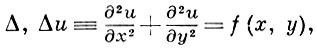
если D_U - замкнутый квадрат |х| ≤ 1, |y| ≤ 1, a D_p - его внутренность x < 1, |y| < 1. Задается h = 1/N, N - натуральное, и строится сетка, причем к D_hU относятся точки

(x, y) = (mh, nh), |mh| ≤ 1, |nh| ≤ 1,

а к D_hF - точки

(x, y) = (mh, nh), |mh| < 1, |nh| < 1,

где m и n - целые. Так как

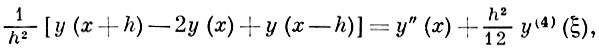
то Δ на достаточно гладких функциях аппроксимируется со вторым порядком разностным оператором L_h, если положить в точках D_hF :

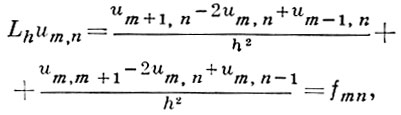
где u_{m, n} и f_{m, n} - значения функций [u]_h и f_h в точке (mh, nh).

Существуют отличные от указанного способы построения операторов L_h, аппроксимирующих оператор L на решениях u дифференциального уравнения L_u = 0 и удовлетворяющих дополнительным требованиям.

Лит. : [1] Филиппов А. Ф., «Докл. АН СССР», 1955 т. 100, № 6, с. 1045-48; [2] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966.

В. С. Рябенький.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.