АППРОКСИМАТИВНЫЙ ПРЕДЕЛ

Расстановка ударений: АППРОКСИМАТИ`ВНЫЙ ПРЕДЕ`Л

АППРОКСИМАТИВНЫЙ ПРЕДЕЛ - предел функции f(x) при х → x₀ по множеству Е, для к-рого х₀ является плотности точкой. В простейшем случае f(х) есть действительная функция точки n-мерного евклидова пространства (в более общем случае - вектор-функция). А. п. обозначается

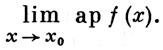
Из существования А. п., вообще говоря, не следует существование обычного предела. Для А. п. имеют место элементарные свойства пределов - единственность, теоремы о пределе суммы, разности, произведения и частного двух функций.

Пусть х₀ - точка плотности области определения действительной функции f(x). Если при этом существует обычный предел 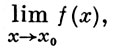, то существует и равный ему А. п. Верхним А. п. функции f(x) в точке х₀ наз. нижняя грань множества чисел у (причем y = + ∞ не исключается), для к-рых множество {х: f(x) > y} имеет х₀ своей точкой разряжения. Аналогично, нижним А. п. функции f(x) в точке х₀ наз. верхняя грань множества тех у (y = - ∞ не исключается), для к-рых х₀ служит точкой разряжения множества {х: f(x) < y}. Эти А. п. обозначаются соответственно

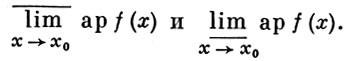
А. п. существует в том и только том случае, если верхний и нижний А. п. равны; их общее значение совпадает с А. п.

В случае действительного х употребляются также односторонние (правый и левый) верхние и нижние А. п. (при этом требуется, чтобы х₀ была соответственно правосторонней или левосторонней точкой плотности области определения функции). Для правого верхнего А. п. употребляют запись

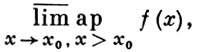
аналогично записываются и другие случаи. При совпадении правых верхнего и нижнего А. п. получается правый А. п., при совпадении левых - левый А. п.

А. п. был использован впервые А. Данжуа (A. Denjoy, 1915) и А. Я. Хинчиным (1916-18) при исследовании дифференциальных связей неопределенного интеграла (в смысле Лебега ив смысле Данжуа-Хинчина) и подинтегральной функции (см. Аппроксимативная непрерывность, Аппроксимативная производная).

Лит. : [1] Сакс С., Теория интеграла, пер. с англ., М., 1949.

Г. П. Толстов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.