АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ

Расстановка ударений: АППРОКСИМАТИ`ВНАЯ ДИФФЕРЕНЦИ`РУЕМОСТЬ

АППРОКСИМАТИВНАЯ ДИФФЕРЕНЦИРУЕМОСТЬ - обобщение понятия дифференцируемости с заменой обычного предела аппроксимативным пределом. Действительная функция f(х) действительного переменного наз. аппроксимативно дифференцируемой в точке х₀, если существует такое число А, что

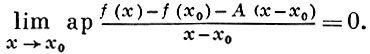
При этом величина А (х - х₀) наз. аппроксимативным дифференциалом функции f(х) в точке х₀ . Функция f(x) аппроксимативно дифференцируема в точке х0 в том и только том случае, если она имеет в этой точке аппроксимативную производную f'_ap (x₀) = A. Аналогично определяется А. д. для действительных функций n действительных переменных. Напр., в случае n = 2, f(x, у) наз. аппроксимативно дифференцируемой в точке (х₀, у₀), если

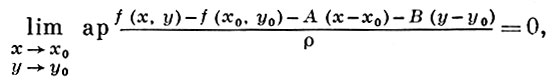
где А и В - нек-рые числа, 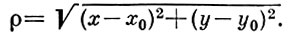. Выражение А(х - х₀) + B(у - у₀) наз. аппроксимативным дифференциалом функции f(х, у) в точке (х₀, у₀).

Теорема Степанова: действительная функция f(x, у), измеримая на множестве Е, аппроксимативно дифференцируема почти всюду на Е в том и только том случае, если почти всюду на Е она имеет конечные аппроксимативные частные производные по x и по y; эти частные производные почти всюду на Е совпадают соответственно с коэффициентами А и В аппроксимативного дифференциала.

Понятие А. д. распространяется также на вектор-функции одного или нескольких действительных переменных.

Лит. : [1] Сакс С., Теория интеграла, пер. с англ., М., 1949.

Г. П. Толстов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.