АППЕЛЯ УРАВНЕНИЯ

Расстановка ударений: А`ППЕЛЯ УРАВНЕ`НИЯ

АППЕЛЯ УРАВНЕНИЯ - обыкновенные дифференциальные уравнения, описывающие движения как голономных, так и не голономных систем, установленные П. Аппелем [1]. Иногда А. у. наз. уравнениями Гиббса-Аппеля, т. к. для голономных систем ранее их установил Дж. У. Гиббс [3]. А. у. в независимых лагранжевых координатах q_s (s = 1, ..., n) имеют вид уравнений 2-го порядка

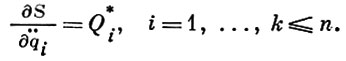
(1)

Здесь

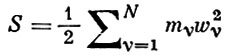
(m_ν и w_ν - массы и ускорения N точек системы) - энергия ускорений системы, выраженная таким образом, чтобы она содержала вторые производные только от координат q_i, i = 1, ..., k, вариации к-рых рассматриваются как независимые, Q*_i - обобщенные силы, соответствующие координатам q_i, получаемые как коэффициенты при независимых вариациях δ q_i в выражении суммы элементарных работ заданных активных сил F_ν на возможных перемещениях δ r_ν :

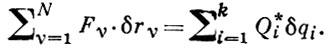
При вычислении S и Q*_i зависимые qׂ_j (δ q_j) (j = k + 1, ..., n) выражаются через независимые скорости (вариации) разрешением n - k уравнений неголономных связей (см. Неголономные системы), выраженных в обобщенных координатах q_s (и уравнений для δ q_s, получаемых из последних). Дифференцированием по времени t найденных выражений для qׂ_j - получаются выражения qׂ ׂ_j через qׂ ׂ_i .

Уравнения (1) совместно с n - k уравнениями неинтегрируемых связей образуют систему (порядка n + k) дифференциальных уравнений для n неизвестных q_s .

В случае голономной системы k = n, все скорости q_s и вариации δ q_s независимы, Q*_i = Q_i и уравнения (1) представляют собой иную запись Лагранжа уравнений 2-го рода.

А. у. в квазикоординатах π_r, где

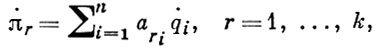
(2)

имеют вид

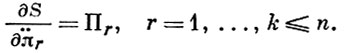
(3)

Здесь S - энергия ускорений, выраженная через вторые производные π ׂ ׂ_r по времени от квазикоординат, n_r - обобщенные силы, соответствующие квазикоординатам. Уравнения (3) совместно с n - k уравнениями неинтегрируемых связей и к уравнениями (2) образуют систему n + k дифференциальных уравнений 1-го порядка относительно такого же числа неизвестных q_s, s = 1, ..., n, и π ׂ_r, r = 1, ..., k.

А. у. являются наиболее общими уравнениями движения механич. систем.

Лит. : [1] Appell P. Е., «Соmр. Rend. », 1899, t. 129; [2] его же, «J. reine und angew. Math. », 1900, Bd 122, S. 205-08; [3] Gibbs J. W., «Аmеr. J. Math. », 1879, v. 2, p. 49-64.

В. В. Румянцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.