АППЕЛЯ МНОГОЧЛЕНЫ

Расстановка ударений: А`ППЕЛЯ МНОГОЧЛЕ`НЫ

АППЕЛЯ МНОГОЧЛЕНЫ, Аппеля полиномы, - класс многочленов над полем комплексных чисел, содержащий многие классич. системы многочленов. А. м. введены П. Аппелем [1]. Последовательность А. м. {A_n (z)}^∞_{n = 0} определяется формальным равенством

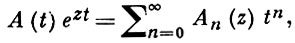
(1)

в к-ром 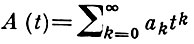- формальный степенной ряд с комплексными коэффициентами a_k, k = 0, 1, 2, ..., причем а₀ ≠ 0. В явном виде А. м. А_n (z) выражаются через числа a_k следующим образом:

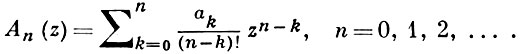
Условие а₀ ≠ 0 равносильно тому, что степень многочлена A_n (z) равна n.

Имеется другое, эквивалентное определение А. м. Пусть

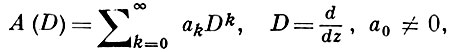
- дифференциальный оператор, вообще говоря, бесконечного порядка, определенный над алгеброй Р комплексных многочленов переменного z = x + iy. Тогда

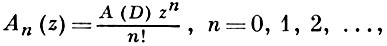
то есть A_n (z) представляет собой образ функции zⁿ /n! при отображении р = А (D)q, р, q ∈ P.

Класс А. м. определяется как совокупность всевозможных систем многочленов {А_n (z)} с производящими функциями вида (1). Принадлежность системы {P_n (z)} многочленов (степени n) классу A⁽¹⁾ равносильна выполнению соотношений

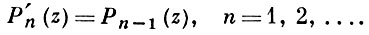
Иногда при определении А. м. класса А⁽¹⁾ пользуются соотношениями

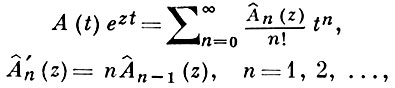
к-рые, с точностью до нормировки, эквивалентны приведенным выше.

А. м. класса A⁽¹⁾ используются при решении уравнений вида

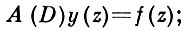
(2)

формальное равенство y(z) = f(z)/A(D) при

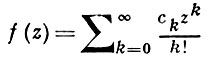
позволяет записать решение (2) в виде

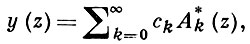
где {A*_k {z)} - А. м. с производящей функцией e^zt /A (t). В связи с этим особый интерес представляют разложения аналитич. функций в ряды по А. м. Кроме того, А. м. находят применение в различных задачах, относящихся к функциональным уравнениям, в том числе к дифференциальным уравнениям, отличным от (2), в вопросах интерполирования, теории приближения, в методах суммирования и др. (см., напр., [1]-[6]). С более общей позиции теория А. м. класса A⁽¹⁾ (и нек-рые приложения) изложена в [6].

А. м. класса А⁽¹⁾ содержат в качестве частных случаев целый ряд классических последовательностей многочленов. Примерами, с точностью до нормировки, могут служить Бернулли многочлены

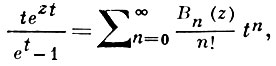
Эрмита многочлены

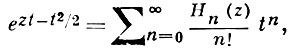
Лагерра многочлены

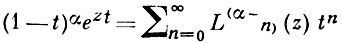
и т. д. Многочисленные примеры А. м. имеются в [2] и [3].

Существуют различные обобщения А. м., к-рые также носят назв. систем А. м. Сюда относятся А. м. с производящими функциями вида

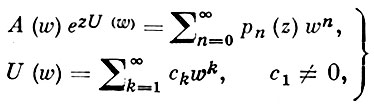
(3)

а также А. м. с производящими функциями более общего характера:

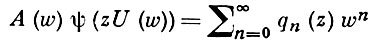
(4)

(см., напр., [2] и [3]). Если w(u) - функция, обратная функции u(w), то принадлежность системы многочленов {p_n (z)}^∞_{n = 0} к классу последовательностей А. м. с производящей функцией вида (3) равносильна выполнению соотношений

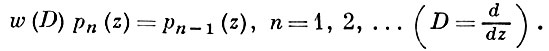
Имеется всего пять ортогональных с весом систем последовательностей А. м. на действительной оси, с производящими функциями вида (3); в том числе среди А. м. с производящими функциями вида (1) лишь одна система многочленов Эрмита является ортогональной с весом е^{- x2 /2} на действительной оси (см. [7]).

О разложениях в ряды по А. м. с производящими функциями вида (3) и (4), а также о связи этих А. м. с различными функциональными уравнениями см. [2],

Класс А^(p) р ≥ 1 - целое, А. м. определяется следующим образом: это есть множество всех систем многочленов {A_n (z)}, для каждой из к-рых имеет место (формальное) представление

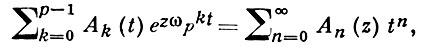
где ω_p = е^{2π i/p}, a A_k (t), k = 0, 1, 2, ..., р - 1 - формальные степенные ряды, свободные члены к-рых таковы, что степень многочлена A_n (z) равна n. Принадлежность последовательности {Q_n (z)} многочленов степени n классу A^(p) равносильна выполнению соотношений 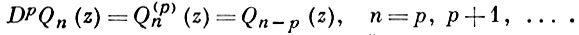Вопросы разложения аналитич. функций в ряды по А. м. класса А^(p) исследованы в [9]. Они тесно примыкают к задаче о нахождении аналитич. решений функциональных уравнений вида

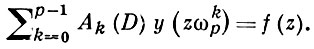
А. м. от двух переменных введены П. Аппелем [10]. Они определяются равенствами

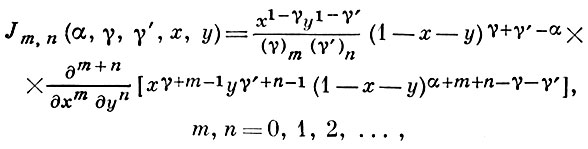
в к-рых полагают (γ)₀ = 1, (γ)_n = γ (γ + 1)...(γ + n - 1) для n ≥ 1; эти А. м. представляют собой аналог Якоби многочленов. А. м. J_{m, n} ортогональны с весом

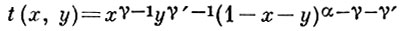
любому многочлену от двух переменных, степени, меньшей m + n, по области T, где Т-треугольник: х > 0, у > 0, х + y < 1; однако они не образуют системы функций, ортогональных с весом t(x, y) в области Т (см., напр., [3]).

Лит. : [1] Appell Р., «Аnn. sci. Ecole norm. super. », 1880, v. 9, p. 119-44; [2] Boas R. P., Buck R. C, Polynomial expansions of analytic functions, В., 1958; [3] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., т. 1-3, М., 1965-67; [4] Wood В., «SIAM J. Appl. Math. », 1969, v. 17, № 4, p. 790-801; [5] Сeгe Г., Ортогональные многочлены, пер. с англ., М., 1962; [6] Бурбаки Н., Функции действительного переменного, пер. с франц., М., 1965; [7] Меiхnеr J., «J. London Math. Soc. », 1934, v. 9, pt 1, p. 6-13; [8] Anderson Ch. A., «J. Math. Analysis and Appl. », 1967, v. 19, № 3, p. 475-91; [9] Казьмин Ю. А., «Матем. заметки», 1969, т. 5, в. 5, с. 509-520; 1969, т. 6, в. 2, с. 161-72; [10] Арреll P., «Arch. Math. Phys. », 1881, Bd 66, S. 238-45.

Ю. А. Казьмин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.