АНТАГОНИСТИЧЕСКАЯ ИГРА

Расстановка ударений: АНТАГОНИСТИ`ЧЕСКАЯ ИГРА`

АНТАГОНИСТИЧЕСКАЯ ИГРА - игра двух участников с прямо противоположными интересами. Формально эта противоположность означает, что при переходе от одной игровой ситуации к другой увеличение выигрыша одного из игроков влечет численно равное уменьшение выигрыша другого, так что во всех ситуациях сумма выигрышей игроков постоянна (можно считать, что эта сумма равна нулю, т. е. что выигрыш одного игрока равен проигрышу другого). Поэтому А. и. наз. также играми двух лиц с нулевой суммой. Математич. понятие антагонистичности (равенство по величине и противоположность по знаку функции выигрыша) является формальным понятием, отличающимся от содержательного философского понятия. Если в А. и. в результате к.-л. переговоров и соглашений один из игроков смог бы увеличить свой выигрыш на нек-рую сумму, то его противник потерял бы такую же сумму. Следовательно, любые соглашения оказываются невыгодными для одного из игроков и потому невозможными. Реальными конфликтными ситуациями, для к-рых А. и. служат достаточно адекватными моделями, являются нек-рые (но не все) военные операции, спортивные и салонные игры, а также ситуации, связанные с принятием деловых решений в условиях конкуренции. Игры против природы и вообще принятие решений в условиях неопределенности (см. Статистическая игра) можно рассматривать как А. и. в предположении, что истинная закономерность природы, неизвестная игроку, приведет к действиям, наименее благоприятным для него.

Задание А. и. в нормальной форме (см. Игр теория) сводится к заданию множеств стратегий А и В соответственно игроков I и II и функции выигрыша Н игрока I, определенной на множестве всех ситуаций А × В (функция выигрыша игрока II равна, по определению А. и., - H). Формально А. и. Г записывается как тройка Г = 〈 A, В, H〉. Процесс разыгрывания игры Г состоит в выборе игроками нек-рых своих стратегий а ∈ А, b ∈ В, после чего игрок I получает от игрока II сумму H(а, b). Это определение А. и. является достаточно общим, чтобы при должном описании множеств стратегий и функции выигрыша охватить все варианты А. и., включая динамические игры, дифференциальные игры и позиционные игры. Разумные действия игроков в А. и. осуществляются на основании принципа минимакса: если

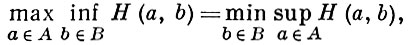
(1)

или

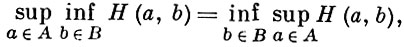
(1')

то в игре Г существуют оптимальные стратегии (ε - оптимальные стратегии) у обоих игроков. Общее значение обеих частей равенства (1') наз. значением игры Г. Однако равенство (1) или (1') уже в самых простых случаях может не иметь места. Напр., в матричной игре с матрицей выигрышей

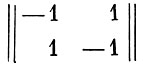
имеют место равенства

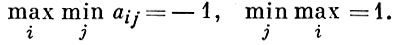
Поэтому множества стратегий игроков расширяются до множества смешанных стратегий, состоящих в случайном выборе игроками своих первоначальных стратегий, наз. чистыми, а функция выигрыша определяется как математич. ожидание выигрыша в условиях применения смешанных стратегий. В приведенном примере оптимальными смешанными стратегиями игроков являются выборы игроками обеих своих стратегий с вероятностями 1/2, а значение игры в смешанных стратегиях равно нулю. Если множества А и В конечны, то А. и. наз. матричной игрой; для нее всегда существуют значение игры и оптимальные смешанные стратегии у каждого из игроков. Если оба множества А и В бесконечны, то оптимальные (и даже ε-оптимальные) смешанные стратегии существуют не всегда (см. Бесконечная игра).

Лит. : [1] Карлин С. Математические методы в теории игр, программировании и экономике, пер. с англ., М., 1964; [2] Партхасаратхи Т., Рагхаван Т., Некоторые вопросы теории игр двух лиц, пер. с англ., М., 1974.

Е. Б. Яновская.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.